题目内容
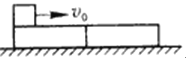
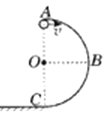
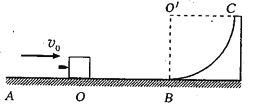
【题目】如图所示，AOB是光滑水平轨道，BC是半径为R的光滑的
固定圆弧轨道，两轨道恰好相切于B点。质量为M的小木块静止在O点，一颗质量为m的子弹以某一初速度水平向右射入小木块内，并留在其中和小木块一起运动，且恰能到达圆弧轨道的最高点C（木块和子弹均看成质点）。
①求子弹射入木块前的速度。
②若每当小木块返回到O点或停止在O点时，立即有一颗相同的子弹射入小木块，并留在其中，则当第9颗子弹射入小木块后，小木块沿圆弧轨道能上升的最大高度为多少？
【答案】（1）
（2）
【解析】试题分析：（1）第一颗子弹射入木块的过程，系统动量守恒，以子弹的初速度方向为正方向，由动量守恒定律得：mv0=（m+M） v1
系统由O到C的运动过程中机械能守恒，由机械能守恒定律得：
（m+M） v12=（m+M）gR
由以上两式解得：v0=
（2）由动量守恒定律可知，第2、4、6…颗子弹射入木块后，木块的速度为0，第1、3、5…颗子弹射入后，木块运动．当第9颗子弹射入木块时，以子弹初速度方向为正方向，
由动量守恒定律得：mv0=（9m+M） v9
设此后木块沿圆弧上升的最大高度为H，由机械能守恒得：（9m+M） v92=（9m+M）gH
由以上各式可得：H=
R
练习册系列答案
相关题目
