题目内容
4. 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=$\sqrt{10}$ m/s | B. | vc=3 m/s | ||
| C. | de=3 m | D. | 从d到e所用时间为4 s |
分析 根据连续相等时间内的位移之差是一恒量求出小球向上做匀减速运动的加速度,根据某段时间内的平均速度等于中间时刻的瞬时速度求出c点的速度,从而结合速度时间公式求出a、d点的速度,根据速度时间公式求出d到e的时间,结合速度位移公式求出d到e的距离.
解答 解:B、根据${x}_{cd}-{x}_{ac}=a{T}^{2}$得小球向上做匀变速直线运动的加速度为:a=$\frac{5-7}{4}m/{s}^{2}=-0.5m/{s}^{2}$,c点的速度为:${v}_{c}=\frac{{x}_{ad}}{2T}=\frac{12}{4}m/s=3m/s$,故B正确.
A、根据速度时间公式得,b点的速度根据速度位移公式可知${2ax}_{bc}{=v}_{c}^{2}{-v}_{b}^{2}$,解得:${v}_{b}=\sqrt{10}$m/s,故A正确.
C、d点的速度vd=vc+aT=3-0.5×2m/s=2m/s,则de间的距离为:${x}_{de}=\frac{0{-v}_{d}^{2}}{2a}=\frac{0-{2}^{2}}{2×(-0.5)}=4m$,故C错误.
D、d到e的时间为:$t=\frac{0-{v}_{d}}{a}=\frac{0-2}{-0.5}s=4s$,故D正确.
故选:ABD.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
15.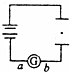 如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
 如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )| A. | 电容器带电量不变 | B. | 尘埃仍静止 | ||
| C. | 电流计中有a→b的电流 | D. | 电流计中有b→a的电流 |
12.某电力公司曾举办“计量日进您家”活动,免费上门为市民做出家庭用电耗能诊断分析,针对每户家庭提出个性化的节能建议.在上门实测过程中,电力技术人员发现,家电待机耗电成为最容易被市民忽略的问题.以电视机为例,待机一天的耗电量在0.2度左右,小小机顶盒一天待机耗电量更是高达0.4度.根据专家统计:每使用l度(千瓦时)电,就相应消耗了0.4kg标准煤,同时产生0.272kg碳粉尘、0.997kg二氧化碳、0.03kg二氧化硫、0.015kg氮氧化物,根据下表提供的数据,估算一户普通家庭待机一年相应产生的二氧化碳为( )
| 每户普通家庭家用电器平均数 | 一台台式电脑 | 2台平板电视机 | 2台空调 | 1台洗衣机 |
| 每台电器待机平均功率(w) | 4 | 1 | 4 | 2 |
| A. | 1.4kg | B. | 14kg | C. | 140kg | D. | 1400kg |
19.关于电场中电荷的电势能的大小,下列说法正确的是( )
| A. | 在电场强度越大的地方,电荷的电势能也越大 | |
| B. | 正电荷沿电场线移动,电势能一定增大 | |
| C. | 负电荷沿电场线移动,电势能一定增大 | |
| D. | 正电荷沿电场线移动,电势能一定减小 |
9.一质点绕半径为R的圆周运动了1$\frac{1}{4}$圈,其路程和位移大小为( )

| A. | $\frac{5πR}{2}$、$\sqrt{2}$R | B. | $\sqrt{2}$R、$\frac{5πR}{2}$ | C. | $\frac{πR}{2}$、$\frac{πR}{2}$ | D. | $\frac{5πR}{2}$、R |
16.关于电磁波谱,下列说法中正确的是( )
| A. | X射线对生命物质有较强的作用,过量的X射线辐射会引起生物体的病变 | |
| B. | γ射线是波长最短的电磁波,它比X射线的频率还要高 | |
| C. | 紫外线比紫光更容易发生干涉和衍射 | |
| D. | 在电磁波谱中,最容易发生衍射现象的是γ射线 | |
| E. | 在电磁波谱中,无线电波一般可用于通信 |
13.物体做匀加速直线运动,已知加速度为5m/s2,那么( )
| A. | 在任意1 s内,物体的末速度一定等于初速度的5倍 | |
| B. | 在任意时间内,物体的末速度一定比初速度大5m/s | |
| C. | 在任意1s内,物体的末速度一定比初速度小5m/s | |
| D. | 第ns的初速度一定比第(n+1)s的末速度小10m/s |
