题目内容
处于静止状态的某原子核X,发生α衰变后变成质量为M的原子核Y,被释放的α粒子垂直射人磁感强度为B的匀强磁场中,测得其圆周与运动的半径为r,设α粒子质量为m,质子的电量为e,试求:
(1)衰变后α粒子的速率υa和动能Eka;
(2)衰变后Y核的速率υy和动能Eky;
(3)衰变前X核的质量Mx.
(1)衰变后α粒子的速率υa和动能Eka;
(2)衰变后Y核的速率υy和动能Eky;
(3)衰变前X核的质量Mx.
(1)α粒子在匀强磁场中做圆周与运动所需的向心力同洛仑兹力提供,
即Bqv=m
,α粒子的带电量为q=2e
所以α粒子的速率:vα=
,
动能:Ekα=
mv
=
(2)由动量守恒mvα-Mvy=0
所以vy=
,
Eky=
Mv
=
(3)由质能方程:△E=△mc2,
而△E=Ekx+Eky,
所以△m=
(
+
)
衰变前X核的质量:Mx=m+M+△m=m+M+
(
+
).
答:(1)衰变后α粒子的速率υa为
,动能Eka为
;
(2)衰变后Y核的速率υy为=
,动能Eky为
;
(3)衰变前X核的质量Mx为m+M+
(
+
).
即Bqv=m
| ||
| r |
所以α粒子的速率:vα=
| 2Ber |
| m |
动能:Ekα=
| 1 |
| 2 |
| 2α |
| 2B2e2r2 |
| m |
(2)由动量守恒mvα-Mvy=0
所以vy=
| 2Ber |
| m |
Eky=
| 1 |
| 2 |
| 2y |
| 2B2e2r2 |
| M |
(3)由质能方程:△E=△mc2,
而△E=Ekx+Eky,
所以△m=
| 2B2e2r2 |
| c2 |
| 1 |
| m |
| 1 |
| M |
衰变前X核的质量:Mx=m+M+△m=m+M+
| 2B2e2r2 |
| c2 |
| 1 |
| m |
| 1 |
| M |
答:(1)衰变后α粒子的速率υa为
| 2Ber |
| m |
| 2B2e2r2 |
| m |
(2)衰变后Y核的速率υy为=
| 2Ber |
| m |
| 2B2e2r2 |
| M |
(3)衰变前X核的质量Mx为m+M+
| 2B2e2r2 |
| c2 |
| 1 |
| m |
| 1 |
| M |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目





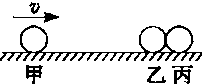
 块与长木板发生相对运动的整个过程中,系统因摩擦产生热量Q=12J。求:
块与长木板发生相对运动的整个过程中,系统因摩擦产生热量Q=12J。求: