题目内容
5.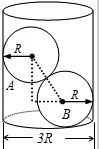 一个直径为3R光滑容器内盛有两个半径均为R的钢球A、B,如图所示,钢球的质量m=0.6kg,重力加速度g=10m/s2,则下列说法正确的是( )
一个直径为3R光滑容器内盛有两个半径均为R的钢球A、B,如图所示,钢球的质量m=0.6kg,重力加速度g=10m/s2,则下列说法正确的是( )| A. | 球A对竖直容器壁压力F1=4$\sqrt{3}$N | B. | 球A对B球的压力F2=4$\sqrt{3}$N | ||
| C. | 球B对竖直容器壁压力F3=2$\sqrt{3}$N | D. | 球B对容器底面的压力F4=2$\sqrt{3}$N |
分析 隔离对A球受力分析,可知两球间的弹力大小以及A受墙壁的压力,对AB整体受力分析,整体受力平衡,根据水平方向和竖直方向受力平衡结合牛顿第三定律列式求解即可.
解答 解:A、以A为研究对象
G=mg=6N
将重力按效果分解F1和F2
由几何关系知α=30°
得:
F1=mgtanα
F2=$\frac{mg}{cosα}$
代入数据得:
F1=2$\sqrt{3}$N,F2=4$\sqrt{3}$N,故A错误,B正确;
C、对AB整体受力分析,整体受力平衡,则可知,竖直容器对B的压力等于竖直容器对A的压力,结合牛顿第三定律可知,F3=F1=2$\sqrt{3}$N,
容器地面对B的支持力等于AB两球的重力,结合牛顿第三定律可知,F4=2mg═12N,故C正确,D错误.
故选:BC
点评 该题主要考查了共点力平衡条件的直接应用,应用整体法可得出容器底面的弹力的大小和左右两侧的弹力大小关系,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.在地球上发射飞行器的三个宇宙速度的示意图如图所示,下面相关说法正确的是( )
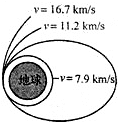

| A. | v=7.9km/s是第一宇宙速度,是飞行器在地球周围空间飞行的最大速度 | |
| B. | v=11.2km/s是第二宇宙速度,以该速度发射的飞行器可以克服地球引力离开地球 | |
| C. | v=16.7km/s是第三宇宙速度,以该速度发射的飞行器可以挣脱太阳引力的束缚,飞到太阳系外 | |
| D. | 当发射速度介于v=7.9km/s与v=11.2km/s之间时,飞行器将绕地球在更高轨道上做圆周运动 |
13.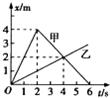 如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
 如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )| A. | 甲、乙两物体始终同向运动 | B. | 4s时甲、乙两物体之间的距离最大 | ||
| C. | 甲的平均速度等于乙的平均速度 | D. | 甲、乙两物体之间的最大距离为4m |
20.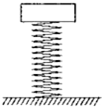 如图所示,一轻质弹簧的下端固定在水平面上,若上端轻放一质量为m的物体甲(物体与弹簧不连接,重力加速度为g,不计阻力),当甲下降h时,其速度变为零;若上端轻放一质量为2m的物体乙,当乙也下降h时,下列说法正确的是( )
如图所示,一轻质弹簧的下端固定在水平面上,若上端轻放一质量为m的物体甲(物体与弹簧不连接,重力加速度为g,不计阻力),当甲下降h时,其速度变为零;若上端轻放一质量为2m的物体乙,当乙也下降h时,下列说法正确的是( )
 如图所示,一轻质弹簧的下端固定在水平面上,若上端轻放一质量为m的物体甲(物体与弹簧不连接,重力加速度为g,不计阻力),当甲下降h时,其速度变为零;若上端轻放一质量为2m的物体乙,当乙也下降h时,下列说法正确的是( )
如图所示,一轻质弹簧的下端固定在水平面上,若上端轻放一质量为m的物体甲(物体与弹簧不连接,重力加速度为g,不计阻力),当甲下降h时,其速度变为零;若上端轻放一质量为2m的物体乙,当乙也下降h时,下列说法正确的是( )| A. | 甲下降过程中先加速再减速 | |
| B. | 甲下降过程中甲与弹簧、地球所组成的系统总势能逐渐减小 | |
| C. | 乙下降过程中先失重再超重后失重 | |
| D. | 乙下降h时,速度大小为2$\sqrt{gh}$ |
10.若某物体做直线运动的v-t图象如图所示,则下列说法中正确的是( )


| A. | t=3s时物体运动的速度方向发生改变 | |
| B. | t=3s时物体运动的加速度方向发生改变 | |
| C. | t=3s时物体离出发点最远 | |
| D. | t=3s时物体的加速度为零t= |
17. 如图所示,在水平向右、大小为E的匀强电场中,在O点固定一电荷量为Q的正电荷,A、B、C、D为以O为圆心、半径为r的同一圆周上的四点,B、D连线与电场线平行,A、C连线与电场线垂直.则( )
如图所示,在水平向右、大小为E的匀强电场中,在O点固定一电荷量为Q的正电荷,A、B、C、D为以O为圆心、半径为r的同一圆周上的四点,B、D连线与电场线平行,A、C连线与电场线垂直.则( )
 如图所示,在水平向右、大小为E的匀强电场中,在O点固定一电荷量为Q的正电荷,A、B、C、D为以O为圆心、半径为r的同一圆周上的四点,B、D连线与电场线平行,A、C连线与电场线垂直.则( )
如图所示,在水平向右、大小为E的匀强电场中,在O点固定一电荷量为Q的正电荷,A、B、C、D为以O为圆心、半径为r的同一圆周上的四点,B、D连线与电场线平行,A、C连线与电场线垂直.则( )| A. | A点的场强大小为$\sqrt{{E}^{2}+{k}^{2}\frac{{Q}^{2}}{{r}^{4}}}$ | B. | B点的场强大小为E-k$\frac{Q}{{r}^{2}}$ | ||
| C. | D点的场强大小不可能为0 | D. | A、C两点的场强相同 |
 纪念中国人民抗日战争暨世界反法西斯战争胜利70周年阅兵式于2015年9月3日在北京天安门广场举行,参加阅兵的履带步兵战车方队是履带装备方队中承载员最多的方队.他们驾驶04A型履带步兵战车第3个通过天安门,该步兵战车作为装甲步兵信息化条件下机动突击作战的新型主战装备,首次亮相阅兵,在某次训练过程中,重2.5×104kg的04A型履带步兵战车以加速度0.6m/s2恒定启动.已知其运行过程中所受阻力恒定为其重力的0.1倍.其匀加速至额定功率400kW后维持额定功率不变加速到最大速度,从启动到最大速度总用时为$\frac{100}{3}$s.求:
纪念中国人民抗日战争暨世界反法西斯战争胜利70周年阅兵式于2015年9月3日在北京天安门广场举行,参加阅兵的履带步兵战车方队是履带装备方队中承载员最多的方队.他们驾驶04A型履带步兵战车第3个通过天安门,该步兵战车作为装甲步兵信息化条件下机动突击作战的新型主战装备,首次亮相阅兵,在某次训练过程中,重2.5×104kg的04A型履带步兵战车以加速度0.6m/s2恒定启动.已知其运行过程中所受阻力恒定为其重力的0.1倍.其匀加速至额定功率400kW后维持额定功率不变加速到最大速度,从启动到最大速度总用时为$\frac{100}{3}$s.求: