��Ŀ����
17�� ��ͼ��ʾ����ˮƽ���ҡ���СΪE����ǿ�糡�У���O��̶�һ�����ΪQ������ɣ�A��B��C��DΪ��OΪԲ�ġ��뾶Ϊr��ͬһԲ���ϵ��ĵ㣬B��D������糡��ƽ�У�A��C������糡�ߴ�ֱ��������
��ͼ��ʾ����ˮƽ���ҡ���СΪE����ǿ�糡�У���O��̶�һ�����ΪQ������ɣ�A��B��C��DΪ��OΪԲ�ġ��뾶Ϊr��ͬһԲ���ϵ��ĵ㣬B��D������糡��ƽ�У�A��C������糡�ߴ�ֱ��������| A�� | A��ij�ǿ��СΪ$\sqrt{{E}^{2}+{k}^{2}\frac{{Q}^{2}}{{r}^{4}}}$ | B�� | B��ij�ǿ��СΪE-k$\frac{Q}{{r}^{2}}$ | ||
| C�� | D��ij�ǿ��С������Ϊ0 | D�� | A��C����ij�ǿ��ͬ |
���� ���ݵ��ɵ糡ǿ�ȹ�ʽE=$\frac{kQ}{{r}^{2}}$�����ʸ���ϳɷ�������⣮
��� �⣺A��������Q��A��ĵ糡ǿ�ȴ�СE��=$\frac{kQ}{{r}^{2}}$������ǿ�糡��A��ĵ糡ǿ�ȴ�СΪE���������ֱ������ʸ���ĺϳɷ�������A��ij�ǿ��СΪ$\sqrt{{E}^{2}+{k}^{2}\frac{{Q}^{2}}{{r}^{4}}}$����A��ȷ��
B��ͬ��������Q��B��ĵ糡ǿ�ȵķ�������ǿ�糡������ͬ�����B��ij�ǿ��СΪE+k$\frac{Q}{{r}^{2}}$����B����
C��������Q��D��ĵ糡ǿ�ȵķ�������ǿ�糡�����෴���Ҵ�С���ʱ����D��ĵ糡ǿ�ȴ�С����Ϊ�㣬��C����
D������ʸ���ĺϳɷ���ϵ��ɵ糡����ǿ�糡�ķ���֪��A��C����ĵ糡ǿ�ȴ�С��ȣ�������ͬ����D����
��ѡ��A��
���� ������ɵĵ糡ǿ�ȹ�ʽ�����ݣ�����ʸ���ϳɷ����Ӧ�ã�ע���������ڸ���ĵ糡ǿ�ȵķ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
5��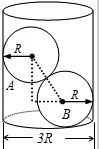 һ��ֱ��Ϊ3R�⻬������ʢ�������뾶��ΪR�ĸ���A��B����ͼ��ʾ�����������m=0.6kg���������ٶ�g=10m/s2��������˵����ȷ���ǣ�������
һ��ֱ��Ϊ3R�⻬������ʢ�������뾶��ΪR�ĸ���A��B����ͼ��ʾ�����������m=0.6kg���������ٶ�g=10m/s2��������˵����ȷ���ǣ�������
 һ��ֱ��Ϊ3R�⻬������ʢ�������뾶��ΪR�ĸ���A��B����ͼ��ʾ�����������m=0.6kg���������ٶ�g=10m/s2��������˵����ȷ���ǣ�������
һ��ֱ��Ϊ3R�⻬������ʢ�������뾶��ΪR�ĸ���A��B����ͼ��ʾ�����������m=0.6kg���������ٶ�g=10m/s2��������˵����ȷ���ǣ�������| A�� | ��A����ֱ������ѹ��F1=4$\sqrt{3}$N | B�� | ��A��B���ѹ��F2=4$\sqrt{3}$N | ||
| C�� | ��B����ֱ������ѹ��F3=2$\sqrt{3}$N | D�� | ��B�����������ѹ��F4=2$\sqrt{3}$N |
2�� ��ͼ��ʾ�����Ϊ30���б��������ˮƽ�����ϣ�һ�������쳤���������˷ֱ�ϵ��С��A�����B������̶���б���嶥�˵�С����O��A������Ϊm��B������Ϊ4m����ʼʱ��������סA��ʹOA����ǡ����ˮƽ��ֱ״̬����������������OB��ƽ����б�棬��ʱB��ֹ��������A�ɾ�ֹ�ͷţ������°ڹ����У�б����ʼ�ձ��־�ֹ���������ж�����ȷ���ǣ�������
��ͼ��ʾ�����Ϊ30���б��������ˮƽ�����ϣ�һ�������쳤���������˷ֱ�ϵ��С��A�����B������̶���б���嶥�˵�С����O��A������Ϊm��B������Ϊ4m����ʼʱ��������סA��ʹOA����ǡ����ˮƽ��ֱ״̬����������������OB��ƽ����б�棬��ʱB��ֹ��������A�ɾ�ֹ�ͷţ������°ڹ����У�б����ʼ�ձ��־�ֹ���������ж�����ȷ���ǣ�������
 ��ͼ��ʾ�����Ϊ30���б��������ˮƽ�����ϣ�һ�������쳤���������˷ֱ�ϵ��С��A�����B������̶���б���嶥�˵�С����O��A������Ϊm��B������Ϊ4m����ʼʱ��������סA��ʹOA����ǡ����ˮƽ��ֱ״̬����������������OB��ƽ����б�棬��ʱB��ֹ��������A�ɾ�ֹ�ͷţ������°ڹ����У�б����ʼ�ձ��־�ֹ���������ж�����ȷ���ǣ�������
��ͼ��ʾ�����Ϊ30���б��������ˮƽ�����ϣ�һ�������쳤���������˷ֱ�ϵ��С��A�����B������̶���б���嶥�˵�С����O��A������Ϊm��B������Ϊ4m����ʼʱ��������סA��ʹOA����ǡ����ˮƽ��ֱ״̬����������������OB��ƽ����б�棬��ʱB��ֹ��������A�ɾ�ֹ�ͷţ������°ڹ����У�б����ʼ�ձ��־�ֹ���������ж�����ȷ���ǣ�������| A�� | ���B�ܵ���Ħ�����ȼ�С������ | |
| B�� | �����б�����Ħ���������Һ����� | |
| C�� | С��A�Ļ�е���غ� | |
| D�� | �����������ܶ�B������ |
6��ijͬѧҪͨ��ʵ�����һ�ڸɵ�صĵ綯�ƺ����裬�ɹ�ѡ��������У���������0��0.6A������ѹ����0��3V��������������R1��10����2A��������������R2��100����2A������ֵ����R0Ϊ1.5�������S���������ɣ�
��1��Ϊ����ʵ��������ܽ�ȷ�ؽ��в���������������Ӧѡ��R1���R1����R2������
��2��������ͼ����ʾʵ�����߽��в���������������±���ʾ�������ݿɿ�������ѹ��ʾ���仯��������Ϊʹ��ѹ����ʾ���仯�����ԣ��뽫ʵ������ͼ�ԼӸĶ����ڷ����л����Ķ����ʵ���·ͼ��

��3��ʵ���иı们������������ֵ�����ݲ�����ݻ�����U-Iͼ����ͼ����ʾ����˸ɵ�ص�����r=0.20������������λ��Ч���֣�
��1��Ϊ����ʵ��������ܽ�ȷ�ؽ��в���������������Ӧѡ��R1���R1����R2������
��2��������ͼ����ʾʵ�����߽��в���������������±���ʾ�������ݿɿ�������ѹ��ʾ���仯��������Ϊʹ��ѹ����ʾ���仯�����ԣ��뽫ʵ������ͼ�ԼӸĶ����ڷ����л����Ķ����ʵ���·ͼ��
| ���� ������ | 1 | 2 | 3 | 4 | 5 |
| I/A | 0.15 | 0.20 | 0.30 | 0.40 | 0.50 |
| U/V | 1.46 | 1.45 | 1.43 | 1.42 | 1.39 |

��3��ʵ���иı们������������ֵ�����ݲ�����ݻ�����U-Iͼ����ͼ����ʾ����˸ɵ�ص�����r=0.20������������λ��Ч���֣�
7�� ��ͼ��ʾ����ԭ��������Ľ�������˷ŵ�һ�������ΪQ��С���Աߣ�������ϸ�Ӧ�����a��b��c��������ij�ǿ��С��ϵ�ǣ�������
��ͼ��ʾ����ԭ��������Ľ�������˷ŵ�һ�������ΪQ��С���Աߣ�������ϸ�Ӧ�����a��b��c��������ij�ǿ��С��ϵ�ǣ�������
 ��ͼ��ʾ����ԭ��������Ľ�������˷ŵ�һ�������ΪQ��С���Աߣ�������ϸ�Ӧ�����a��b��c��������ij�ǿ��С��ϵ�ǣ�������
��ͼ��ʾ����ԭ��������Ľ�������˷ŵ�һ�������ΪQ��С���Աߣ�������ϸ�Ӧ�����a��b��c��������ij�ǿ��С��ϵ�ǣ�������| A�� | Ea=Eb=Ec | B�� | Ea��Eb��Ec | C�� | Ea��Eb��Ec | D�� | ���ж� |