题目内容
2.如图甲,在水平桌面上固定着两根相距L=20cm、相互平行的无电阻轨道P、Q,轨道一端固定一根电阻r=0.02Ω的导体棒a,轨道上横置一根质量m=40g、电阻可忽略不计的金属棒b,两棒相距也为L=20cm.该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中.开始时,磁感应强度B0=0.10T.设棒与轨道间的最大静摩擦力等于滑动摩擦力,g=10m/s2.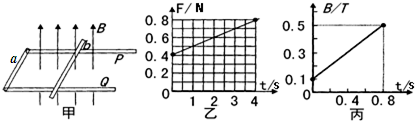
(1)若保持磁感应强度B0的大小不变,从t=0时刻开始,给b棒施加一个水平向右的拉力,使它由静止开始做匀加速直线运动.此拉力F的大小随时间t变化关系如图乙所示.求b棒做匀加速运动的加速度及b棒与导轨间的滑动摩擦力;
(2)若从t=0开始,磁感应强度B随时间t按图丙中图象所示的规律变化,求在金属棒b开始运动前,这个装置释放的热量是多少?
分析 (1)根据F与t的函数表达式,结合牛顿第二定律,及闭合电路欧姆定律,依据图象的含义,即可求解.
(2)根据法拉第定律、欧姆定律和安培力公式,求解在金属棒b开始运动前经过的时间,再由焦耳定律求解热量.
解答 解:(1)由图象可得到拉力F与t的大小随时间变化
的函数表达式为
F=F0+$\frac{△F}{△t}t=0.4+0.1t$
当b棒匀加速运动时,根据牛顿第二定律有:
F-f-F安=ma
F安=B0IL
I=$\frac{E}{r}=\frac{{B}_{0}Lv}{r}$
v=at
∴F安=$\frac{{B}_{0}^{2}{L}^{2}a}{r}t$
联立可解得F=f+ma+$\frac{{B}_{0}^{2}{L}^{2}a}{r}t$
代入数据可解得a=5m/s2 f=0.2N
(2)当磁感应强度均匀增大时,闭合电中和有恒定的感应电流I,以b棒为研究对象,它受到的安培力逐渐增大,静摩擦力也随之增大,当磁感应度增大到b所受安掊力F与最大静摩擦力f相等时开始滑动.
感应电动势:E=$\frac{△B}{△t}{L}^{2}=0.02V$
I=$\frac{E}{r}=1A$
棒b将要运动时,有f=BtIL
∴Bt=$\frac{f}{IL}=1T$
根据Bt=B0+$\frac{△B}{△t}$t=0.1+0.5t,
得:t=1.8s
回路中产生焦耳热为:Q=I2•Rt=12×0.02×1.8=0.036J
答:(1)匀加速运动的加速度是5m/s2,b棒与导轨间的滑动摩擦力是0.2N.
(2)在金属棒b开始运动前,这个装置释放的热量是0.036J
点评 本题考查电磁感应定律中的图象问题,要注意明确图象的斜率含义,掌握牛顿第二定律与闭合电路欧姆定律的应用,注意从图象中选取两点代入公式计算,是解题的关键.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 如图所示,活塞将一定质量的气体封闭在直立圆筒形导热的气缸中,活塞上堆放细砂,活塞处于静止,现对气体缓慢加热,同时逐渐取走细砂,使活塞缓慢上升,直到细砂全部取走,若活塞与气缸之间的摩擦可忽略,则在此过程中( )
如图所示,活塞将一定质量的气体封闭在直立圆筒形导热的气缸中,活塞上堆放细砂,活塞处于静止,现对气体缓慢加热,同时逐渐取走细砂,使活塞缓慢上升,直到细砂全部取走,若活塞与气缸之间的摩擦可忽略,则在此过程中( )| A. | 气体压强可能增大,内能可能不变 | B. | 气体从外界吸热,内能一定增加 | ||
| C. | 气体对外做功,内能一定减小 | D. | 气体对外做功,气体温度可能不变 |
| A. | WF2<9WF1,Wf2=3Wf1 | B. | WF2<9WF1,Wf2<3Wf1 | ||
| C. | WF2>9WF1,Wf2>3Wf1 | D. | WF2>9WF1,Wf2=3Wf1 |
| A. | 地震波是一种复杂的机械波,既有横波又有纵波 | |
| B. | 因为地震波只有纵波,所以破坏性最强 | |
| C. | 地震波传播过程中携带有巨大的能量,传播过程中破坏性很大 | |
| D. | 地震波既有纵波也有横波,且传播速度相等,所以破坏性强 | |
| E. | 地震的震源停止振动时,地震波也立即停止传播,导致受灾范围高度集中 |
 如图所示,某极地轨道卫星的运行轨道平面通过地球的南北两极,已知该卫星从北纬60°的正上方,按图示方向第一次运行到南纬60°的正上方时所用时间为1h,则下列说法正确的是( )
如图所示,某极地轨道卫星的运行轨道平面通过地球的南北两极,已知该卫星从北纬60°的正上方,按图示方向第一次运行到南纬60°的正上方时所用时间为1h,则下列说法正确的是( )| A. | 该卫星与同步卫星的运行半径之比为1:4 | |
| B. | 该卫星与同步卫星的运行速度之比为1:2 | |
| C. | 该卫星的运行速度一定大于7.9km/s | |
| D. | 该卫星的机械能一定大于同步卫星的机械能 |
 星际探测是现代航天科技发展的重要课题.如图,某探测器从空间的O点沿直线ON从静止开始以加速度α作匀加速直线运动,两个月后与地球相遇于P点,再经两个月与地球相遇于Q点,已知引力常量G,地球公转周期为T(12个月),忽略天体对探测器的影响,则可估测太阳质量为( )
星际探测是现代航天科技发展的重要课题.如图,某探测器从空间的O点沿直线ON从静止开始以加速度α作匀加速直线运动,两个月后与地球相遇于P点,再经两个月与地球相遇于Q点,已知引力常量G,地球公转周期为T(12个月),忽略天体对探测器的影响,则可估测太阳质量为( )| A. | $\frac{{{π^2}{α^3}{T^4}}}{3546G}$ | B. | $\frac{{{π^2}{α^3}{T^4}}}{3456G}$ | C. | $\frac{3456G}{{{π^2}{α^3}{T^4}}}$ | D. | $\frac{3546G}{{{π^2}{α^3}{T^4}}}$ |



 如图所示,用销钉固定的光滑活塞把水平放置的气缸分隔成容积相同的A和B两部分,A、B缸内分别封闭有一定质量的理想气体.初始时,两部分气体温度都为t0=27℃,A部分气体压强为PAO=2.5×l05Pa,B部分气体压强为PBO=1.5×l05Pa.拔去销钉后,保持A部分气体温度不变,同时对B部分气体加热,直到B内气体温度上升为t=127℃,停止加热,待活塞重新稳定后,(活塞厚度可忽略不计,整个过程无漏气发生)求:
如图所示,用销钉固定的光滑活塞把水平放置的气缸分隔成容积相同的A和B两部分,A、B缸内分别封闭有一定质量的理想气体.初始时,两部分气体温度都为t0=27℃,A部分气体压强为PAO=2.5×l05Pa,B部分气体压强为PBO=1.5×l05Pa.拔去销钉后,保持A部分气体温度不变,同时对B部分气体加热,直到B内气体温度上升为t=127℃,停止加热,待活塞重新稳定后,(活塞厚度可忽略不计,整个过程无漏气发生)求: U形管两臂粗细不等,左管开口向上,封闭的右管横截面积是开口的左管的3倍,管中装入水银,大气压为P0=76cmHg.开口管中水银面到管口距离为h1=22cm,且水银面比封闭管内高△h=4cm,封闭管内空气柱长为h2=11cm,如图所示.现用小活塞把开口端封住,并缓慢推动活塞,使两管液面相平,推动过程中两管的气体温度始终不变,试求:
U形管两臂粗细不等,左管开口向上,封闭的右管横截面积是开口的左管的3倍,管中装入水银,大气压为P0=76cmHg.开口管中水银面到管口距离为h1=22cm,且水银面比封闭管内高△h=4cm,封闭管内空气柱长为h2=11cm,如图所示.现用小活塞把开口端封住,并缓慢推动活塞,使两管液面相平,推动过程中两管的气体温度始终不变,试求: