题目内容
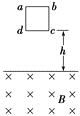
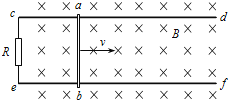
【题目】如图所示，在竖直向下的磁感应强度为B的匀强磁场中，两根足够长的平行光滑金属轨道cd、ef固定在水平面内，相距为L，轨道左端c、e间连接一阻值为R的电阻．将一质量为m的导体棒ab垂直于cd、ef放在轨道上，与轨道接触良好．轨道和导体棒的电阻均不计．
(1)导体棒ab沿轨道以速度v向右做匀速运动．
时，磁感应强度为
，此时ab到达的位置恰好使cabe构成一个边长为L的正方形．为使闭合电路中不产生感应电流，求从开始，磁感应强度B随时间t变化的关系式．
(2)如果匀强磁场的磁感应强度B保持不变，为使导体棒ab沿轨道以速度v向右做匀速运动，需对导体棒ab施加一个水平向右的外力F．
①求外力F的大小；
②通过公式推导验证：在
时间内，外力F对导体棒ab所做的功W等于电路获得的电能
，也等于电阻R中产生的焦耳热Q．
【答案】(1)
(2) ①
②证明过程见解析。
【解析】
(1)要使闭合电路中不产生感应电流，穿过闭合电路的磁通量应保持不变．
时，穿过闭合电路的磁通量
设t时刻匀强磁场的磁感应强度为B，此时的磁通量为：
则
得
(2)①导体棒ab中的感应电流为：
导体棒ab所受的安培力为：
导体棒ab匀速运动，水平外力为：
②导体棒ab匀速运动，有：
在
时间内，外力F对ab所做的功为：
电动势为：
电路获得的电能为：
电阻R中产生的焦耳热为：
可见，外力F对导体棒ab所做的功W等于电路获得的电能
，也等于电阻R中产生的焦耳热Q．
练习册系列答案
相关题目
