题目内容
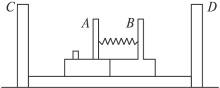
如图6-4-2所示,一质量为m1的半圆形槽内壁光滑,放在光滑水平面上,槽的左侧有一固定的木桩阻止槽水平向左运动,槽的半径为R.今从槽左侧A端的正上方D处自由释放一个质量为m2的小球,球恰好从A点自然进入槽的内壁轨道.试求:
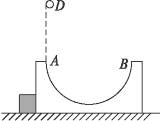
图6-4-2
(1)若D点相对A点的高度为h0,在小球到达槽的最低点的过程中木桩对槽的冲量;
(2)为了使小球沿槽的内壁恰好运动到槽的右端B点,D点到A点的高度h.

图6-4-2
(1)若D点相对A点的高度为h0,在小球到达槽的最低点的过程中木桩对槽的冲量;
(2)为了使小球沿槽的内壁恰好运动到槽的右端B点,D点到A点的高度h.
(1)m2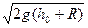 (2)
(2) R
R
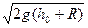 (2)
(2) R
R(1)在小球从D点到达槽最低点的过程中,槽未发生运动,小球机械能守恒
 m2v2=m2g(h0+R)
m2v2=m2g(h0+R)
v=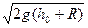
在此过程中对球和槽的水平方向应用动量定理,木桩对槽的冲量
I=m2v-0=m2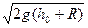 .
.
(2)在球从最低点向B点运动过程中,球、槽系统水平方向动量守恒、机械能也守恒,恰好运动到B点的含义为到达B点时两者速度相等,故有
 m2v02=m2g(h+R)
m2v02=m2g(h+R)
m2v0=(m1+m2)v1
 m2v02=
m2v02= (m1+m2)v12+m2gR
(m1+m2)v12+m2gR
解以上三式可得,h= R.
R.
 m2v2=m2g(h0+R)
m2v2=m2g(h0+R)v=
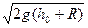
在此过程中对球和槽的水平方向应用动量定理,木桩对槽的冲量
I=m2v-0=m2
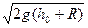 .
.(2)在球从最低点向B点运动过程中,球、槽系统水平方向动量守恒、机械能也守恒,恰好运动到B点的含义为到达B点时两者速度相等,故有
 m2v02=m2g(h+R)
m2v02=m2g(h+R)m2v0=(m1+m2)v1
 m2v02=
m2v02= (m1+m2)v12+m2gR
(m1+m2)v12+m2gR解以上三式可得,h=
 R.
R.
练习册系列答案
相关题目

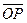 =
= (OP1+OP2+…+OP10)
(OP1+OP2+…+OP10)