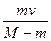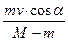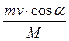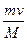题目内容
如图所示,质量为m的小物体(可视为质点)放在小车上,它们一起在两堵竖直墙壁之间运动,小车质量为M,且M>m。设车与物体间的动摩擦因数为μ,车与水平面间无摩擦,车与墙壁碰撞后速度反向而且大小不变,且碰撞时间极短。开始时车紧靠在左面墙壁上,物体位于车的最左端,车与物体以共同速度v0向右运动。若两墙壁之间的距离足够长,求:
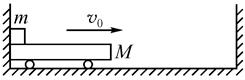
(1)小车与墙壁第2次碰撞前(物体未从车上掉下)的速度;
(2)要使物体不从车上滑落,车长l应满足的条件。

(1)小车与墙壁第2次碰撞前(物体未从车上掉下)的速度;
(2)要使物体不从车上滑落,车长l应满足的条件。
(1)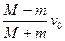
(2)l≥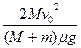
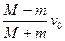
(2)l≥
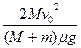
(1)第2次碰前,车与小物体已达到共同速度v1,由动量守恒定律:
(M-m)v0=(M+m)v1
v1=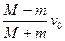 。
。
(2)设第1次碰后小物体相对车向右滑动l1,由能量守恒得:
μmgl1=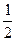 (M+m)v02-
(M+m)v02-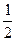 (M+m)v12
(M+m)v12
解得:l1=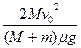
设第2次碰后物体相对车向左运动l2,共同运动的速度为v2,则有:
Mv1-mv1=(M+m)v2
μmgl2=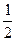 (M+m)v12-
(M+m)v12-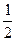 (M+m)v22
(M+m)v22
解得:l2=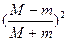 l1<l1
l1<l1
同理可得ln<ln-1,即只要第一次碰撞后小物体不从小车上掉下,以后的碰撞均不能使物体从车上掉下。
所以要使物体不从车上掉下,车长应满足条件:l≥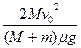 。
。
(M-m)v0=(M+m)v1
v1=
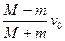 。
。(2)设第1次碰后小物体相对车向右滑动l1,由能量守恒得:
μmgl1=
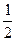 (M+m)v02-
(M+m)v02-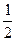 (M+m)v12
(M+m)v12解得:l1=
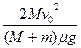
设第2次碰后物体相对车向左运动l2,共同运动的速度为v2,则有:
Mv1-mv1=(M+m)v2
μmgl2=
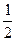 (M+m)v12-
(M+m)v12-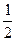 (M+m)v22
(M+m)v22解得:l2=
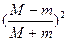 l1<l1
l1<l1同理可得ln<ln-1,即只要第一次碰撞后小物体不从小车上掉下,以后的碰撞均不能使物体从车上掉下。
所以要使物体不从车上掉下,车长应满足条件:l≥
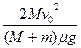 。
。
练习册系列答案
相关题目