题目内容
13．
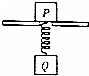如图所示，物体P放在带孔的桌面上，通过弹簧与物体Q相连接．已知GP=2GQ=20N，弹簧的劲度系数为100N/m，若需使物体P离开桌面，则物体Q上移的最小距离为多少？
分析 根据共点力的平衡条件以及胡克定律可明确弹簧的形变量，再根据题意明确Q上升的距离与形变量之间的关系．
解答 解：开始时弹簧使Q保持静止状态；则有：mQg=kx1；
弹簧处于伸长状态；
若要使P离开桌面，则P受到的弹力应向上，故弹簧应处于压缩状态；
则有：mPg=kx2；
Q上滑的距离应为：x=x1+x2
解得：x=0.3m；
答：物体Q至少应上升0.3m．
点评 本题考查胡克定律的应用，要注意明确题意，分析出如何才能使P离开桌面．
练习册系列答案
相关题目
3．气球下悬挂一物体，当气球以20m/s的速度上升到某一高度时，悬线断开，物体最后2s内通过了100m，（忽略空气阻力，g取10m/s2）悬线断开时物体距地面的高度及物体从脱离绳到落地的时间是（ ）
| A． | 320m，8s | B． | 320m，6s | C． | 160m，8s | D． | 160m，6s |
4．
如图所示，质量为m的小球置于光滑的正方体盒子中，盒子的边长略大于球的直径．某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动，已知重力加速度为g，空气阻力不计，要使在最高点时盒子与小球之间恰好无作用力，则（ ）
如图所示，质量为m的小球置于光滑的正方体盒子中，盒子的边长略大于球的直径．某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动，已知重力加速度为g，空气阻力不计，要使在最高点时盒子与小球之间恰好无作用力，则（ ）| A． | 该盒子做匀速圆周运动的周期等于π$\sqrt{\frac{R}{g}}$ | |
| B． | 该盒子做匀速圆周运动的周期等于2π$\sqrt{\frac{R}{g}}$ | |
| C． | 盒子在最低点时盒子与小球之间的作用力大小等于3mg | |
| D． | 盒子在最低点时盒子与小球之间的作用力大小等于5mg |
1．如图所示为单摆在两次受迫振动中的共振曲线，则下列说法正确的是（ ）
| A． | 若两次受迫振动分别在月球上和地球上进行，且摆长相等，则图线Ⅱ是月球上的单摆的共振曲线 | |
| B． | 若两次受迫振动是在地球上同一地点进行，则两次摆长之比为L I：L II=4：25 | |
| C． | 图线Ⅱ若是在地面上完成的，则该摆摆长约为lm | |
| D． | 若外驱动力的频率由0.4Hz变为0.3Hz时，两次受迫振动稳定后的振幅都将会增加 |
如图所示，在光滑的水平面上停有一辆小车，上面站着一个人，人和车的总质量为M，人手上拿一个质量为m的小球，假如人将小球以相对于车的速度v0水平抛出．求：
18．
如图所示，位于水平桌面上的物块P，由跨过定滑轮的轻绳与物块Q相连，从滑轮到P和Q的两段绳都是水平的．已知Q与P之间以及P与桌面之间的动摩擦因数都是μ，P的质量是m，Q的质量是2m，滑轮的质量、滑轮轴上的摩擦都不计．若用一水平向右的力F拉P使它做匀速运动，则F的大小为（ ）
如图所示，位于水平桌面上的物块P，由跨过定滑轮的轻绳与物块Q相连，从滑轮到P和Q的两段绳都是水平的．已知Q与P之间以及P与桌面之间的动摩擦因数都是μ，P的质量是m，Q的质量是2m，滑轮的质量、滑轮轴上的摩擦都不计．若用一水平向右的力F拉P使它做匀速运动，则F的大小为（ ）| A． | 7μmg | B． | 5μmg | C． | 3μmg | D． | μmg |
5．下列关于匀速圆周运动的说法正确的是（ ）
| A． | 物体做圆周运动而产生一个向心力 | |
| B． | 向心力始终指向圆心，所以向心力是恒定的 | |
| C． | 向心加速度只改变线速度的大小 | |
| D． | 向心加速度只改变线速度的方向 |
如图所示，传送带与水平面夹角为θ=37°，以速度v=10m/s匀速运行着．现在传送带的A端轻轻放上一个小物体（可视为质点），已知小物体与传送带之间的摩擦因数μ=0.5，A、B间距离s=16m，则当皮带轮处于下列两情况时，小物体从A端运动到B端的时间分别为多少？已知sin37°=0.6，cos37°=0.8，取g=10m/s2
3．考汽车驾照时需要进行路考，路考中有一项是定点停车．在一次定点停车考试中，某学员驾驶汽车以8m/s的速度匀速行驶，当车头与路旁竖立的标志杆相距20m时，学员立即刹车，让车做匀减速直线运动，结果车头恰好停在标志杆处，忽略学员的反应时间，下列说法正确的是（ ）
| A． | 汽车刹车过程的加速度大小为0.8m/s2 | |
| B． | 汽车刹车过程的加速度大小为1.2m/s2 | |
| C． | 汽车刹车过程的时间为2.5s | |
| D． | 汽车刹车过程的时间为5s |