题目内容
1.如图所示为单摆在两次受迫振动中的共振曲线,则下列说法正确的是( )
| A. | 若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线Ⅱ是月球上的单摆的共振曲线 | |
| B. | 若两次受迫振动是在地球上同一地点进行,则两次摆长之比为L I:L II=4:25 | |
| C. | 图线Ⅱ若是在地面上完成的,则该摆摆长约为lm | |
| D. | 若外驱动力的频率由0.4Hz变为0.3Hz时,两次受迫振动稳定后的振幅都将会增加 |
分析 当受迫振动的频率等于单摆的固有频率,将发生共振,根据共振的频率大小,得出固有周期的大小,根据单摆的周期公式进行分析.
解答 解:A、若两次受迫振动分别在月球上和地球上进行,因为图线Ⅰ单摆的固有频率较小,则固有周期较大,根据T=$2π\sqrt{\frac{L}{g}}$,知,周期大的重力加速度小,则图线Ⅰ是月球上单摆的共振曲线.故A错误.
B、若两次受迫振动均在地球上同一地点进行的,则重力加速度相等,因为固有频率比为2:5,则固有周期比为5:2,根据T=$2π\sqrt{\frac{L}{g}}$,知摆长比为25:4.故B错误.
C、图线Ⅱ若是在地球表面上完成的,则固有频率为0.5Hz,则T=$2π\sqrt{\frac{L}{g}}$=2,解得L=1m.故C正确;
D、若外驱动力的频率由0.4Hz变为0.3Hz时,由图可知,图线Ⅱ的振幅随频率的减小而减小,故D错误.
故选:C.
点评 解决本题的关键知道受迫振动的频率等于驱动力的频率,当驱动力的频率等于固有频率时,发生共振.以及掌握单摆的周期公式.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
11.如图所示为甲、乙两质点运动的位移-时间图象,由图象可知( )


| A. | 甲、乙两质点在1s末时相遇 | |
| B. | 甲做直线运动,乙做往返运动 | |
| C. | 甲、乙两质点在第1s内运动方向相反 | |
| D. | 在第1s内,甲质点的速率比乙质点的速率要大 |
16.以v0的速度水平抛出一物体,当其水平分位移与竖直分位移相等时,下列说法正确的是( )
| A. | 运动的位移是$\frac{2\sqrt{2}{v}_{0}}{g}$ | |
| B. | 竖直分速度的大小等于水平分速度的大小 | |
| C. | 运动的时间是$\frac{2{v}_{0}}{g}$ | |
| D. | 即时速度的大小是2v0 |
6.A、B两球在水平光滑直导轨上同向运动,已知它们的动量分别为PA=5kg•m/s,PB=7kg•m/s,A从后面追上B并发生碰撞,碰后B的动量为P′=10kg•m/s.则两球的质量关系可能为( )
| A. | MA=MB | B. | MB=2MA | C. | MB=3MA | D. | MB=4MA |
11. 如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )
如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )
 如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )
如图所示为大型电子地磅电路图,所用器材均为理想器材,电源电动势为E,内阻不计,不称物体时,滑片P在A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值.若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,己知两只弹簧的总弹力与形变量成正比,比例系数为k,下列说法正确的是( )| A. | 所称重物的重量G与电流大小I的关系为G=2kL-$\frac{EkL}{I{R}_{0}}$ | |
| B. | 若满偏电流为I0,則满偏位置刻重量值为G=2kL+$\frac{EkL}{{I}_{0}{R}_{0}}$ | |
| C. | 重量值的零刻线刻在电流表$\frac{E}{2{R}_{0}}$处 | |
| D. | 增大电流表量程会减小装置的测量精度 |
 有一个物体做直线运动,其速度--时间图象如图所示,从图中判断0-2s,2-4s,4-6s,6-8s各阶段的运动情况.
有一个物体做直线运动,其速度--时间图象如图所示,从图中判断0-2s,2-4s,4-6s,6-8s各阶段的运动情况. 如图所示,光滑水平面上有A、B两个物块,其质量分别为mA=2.0kg,mB=1.0kg,现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度范围内),然后同时释放,弹簧开始逐渐变长.试求当弹簧刚好恢复原长时,A和B物块速度vA、vB的大小.
如图所示,光滑水平面上有A、B两个物块,其质量分别为mA=2.0kg,mB=1.0kg,现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度范围内),然后同时释放,弹簧开始逐渐变长.试求当弹簧刚好恢复原长时,A和B物块速度vA、vB的大小.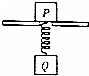 如图所示,物体P放在带孔的桌面上,通过弹簧与物体Q相连接.已知GP=2GQ=20N,弹簧的劲度系数为100N/m,若需使物体P离开桌面,则物体Q上移的最小距离为多少?
如图所示,物体P放在带孔的桌面上,通过弹簧与物体Q相连接.已知GP=2GQ=20N,弹簧的劲度系数为100N/m,若需使物体P离开桌面,则物体Q上移的最小距离为多少? 如图是用双缝干涉测光的波长的实验装置示意图. 图中①是光源,②是凸透镜,⑤是光屏,可知④是双缝.实验中,使用的双缝的间距为0.02cm,测得双缝与光屏之间的距离为50cm.第1级亮纹中心到第5级亮纹中心距离为0.45cm,则待测单色光的波长是450nm.
如图是用双缝干涉测光的波长的实验装置示意图. 图中①是光源,②是凸透镜,⑤是光屏,可知④是双缝.实验中,使用的双缝的间距为0.02cm,测得双缝与光屏之间的距离为50cm.第1级亮纹中心到第5级亮纹中心距离为0.45cm,则待测单色光的波长是450nm.