题目内容
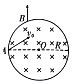
【题目】如图甲所示,真空中两平行金属板A、B水平放置,间距为d,P点在A、B间,A板接地,B板的电势φB随时间t的变化情况如图乙所示,已知φ1<φ2.t=0时,在P点由静止释放一质量为m、电荷量为e的电子,到t=3T时刻,电子回到P点.电子运动过程中始终未与极板相碰,电子重力不计,则下列说法正确的是( )
A. φ1∶φ2=4∶5
B. φ1∶φ2=3∶4.
C. 电子从P点出发至返回P点,动能增加,电势能减少
D. 电子从P点出发至返回P点,动能和电势能都增加
【答案】AD
【解析】
电子在交变电场中运动，先由牛顿第二定律求出加速度，再运动学规律求出末速度和位移，由题设条件解出交变电场正负电势的关系。涉及的电势能问题，由能量守恒可以进行判断.
设电子在0~T时间内的加速度大小为a1，T时刻的速度为v1，T~3T时间内的加速度大小为a2,3T时刻的速度为v2，画出电子在0~3T时间内的v-t图象，如图所示：
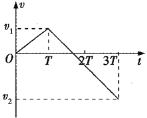
A、B、设电子在0~T时间内的位移为s1，在T~3T时间内的位移为s2，则有
，
，
，其中
，
，联立解得
，
，由于加速度大小
，故
，又匀强电场中
，
，
，故
，则A正确，B错误.
C、D、电势能
，原来在P点时，P点电势大于0，电子电势能为负值，回到P点后，P点电势小于0，电子电势能为正值，故电子从P点出发至返回P点，电子电势能增加，又由可知电子从P点出发至返回P点，动能增加；故C错误，D正确.
故选AD.
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
