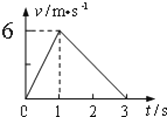
题目内容
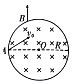
【题目】如图所示，在一个半径为R的圆形区坡内存在微感应强度为B、方向垂直于纸面向里的匀强磁场，一个比荷为
的正粒子，从A点沿与AO夹角
的方向射入匀强磁场区域，最终从B点沿与AO垂直的方向离开磁场。若粒子在运动过程中只受磁场力作用，则
A. 粒子运动的轨道半径
B. 粒子在磁场区域内运动的时间
C. 粒子的初速度的
D. 若仅改变初速度的方向，该粒子仍能从B点飞出磁场区域
【答案】AC
【解析】
粒子在磁场中做匀速圆周运动，速度的偏向角等于轨迹对应的圆心角。画出轨迹，由数学知识求出轨迹半径，再利用洛伦兹力提供向心力结合结合关系即可分析求解，利用周期公式结合粒子在磁场中转过的圆心角，求解粒子在磁场中运动的时间。
A、画出粒子轨迹示意图，如下图所示，
因为粒子从B点沿与AO垂直的方向离开磁场，故OB与AO平行，又因为
OAB与
OAB均为等腰三角形，可得：
OAB=OBA=OBA=OAB，所以OA与BO也平行，因为粒子速度方向偏转的角度为
，故AOB=，所以四边形OAOB为两个等边三角形组成的菱形，故粒子运动的轨道半径r=R，故A正确。
B、粒子在磁场中运动的周期：T=
=
，粒子在磁场中转过的圆心角
=600，所以粒子在磁场中运动的时间为：t=
=
，故B错误。
C、根据洛伦兹力提供向心力可得：qv0B=m
，结合轨道半径r=R，联立可得粒子的初速度为：v0=
，故C正确。
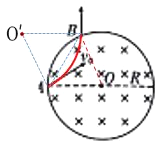
D、当入射粒子速度方向发生变化时，粒子运动的轨迹示意图如图所示，
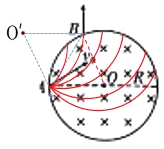
速度大小不变，粒子做圆周运动的半径不变，入射速度方向发生变化，粒子在圆周上的出射点也随之变化，所以若仅改变初速度的方向，该粒子将不能从B点飞出磁场区域，故D错误。
故选：A、C
练习册系列答案
相关题目
