题目内容
12. 如图所示,质量分别为m1=3kg和m2=1kg的两个物体A,B放在固定在地面上的光滑斜面上,斜面倾角为θ=37°,A,B之间的动摩擦因数为μ=0.2,已知最大静摩擦力等于滑动摩擦力,现对A施加一个水平力F使A,B保持相对静止一起沿斜面运动,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求力F的大小范围.
如图所示,质量分别为m1=3kg和m2=1kg的两个物体A,B放在固定在地面上的光滑斜面上,斜面倾角为θ=37°,A,B之间的动摩擦因数为μ=0.2,已知最大静摩擦力等于滑动摩擦力,现对A施加一个水平力F使A,B保持相对静止一起沿斜面运动,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求力F的大小范围.
分析 AB两个物体保持相对静止一起沿斜面运动,则加速度相同,对B进行受力分析,当B受到水平向左的最大静摩擦力时,向上加速度最大,此时F最大,当B受到水平向右的最大静摩擦力时,向下的加速度最大,此时F最小,求出B向上和向下运动的最大加速度,再对AB整体受力分析,根据牛顿第二定律求出F的最大值和最小.
解答 解:对B进行受力分析,受到重力、支持力和静摩擦力,当B受到水平向左的最大静摩擦力时,向上加速度最大,设此时加速度为a1,把加速度进行分解,则有:
水平方向:a1cos37°=μFN,
竖直方向:a1sin37°=FN-m2g
带入数据解得:${a}_{1}=\frac{50}{17}m/{s}^{2}$,
对AB整体受力分析,如图所示:
则有:Fcos37°-(m1+m2)gsin37°=(m1+m2)a1
解得:F=44.7N,
当B受到水平向右的最大静摩擦力时,向下加速度最大,设此时加速度为a2,把加速度进行分解,则有:
水平方向:a2cos37°=μFN′,
竖直方向:a2sin37°=m2g-FN′,
解得:a2=$\frac{50}{23}m/{s}^{2}$
同理对AB整体受力分析,则有:
(m1+m2)gsin37°-F′cos37°=(m1+m2)a2
解得:F′=19.1N
所以力F的大小范围为19.1N≤F≤44.7N
答:力F的大小范围为19.1N≤F≤44.7N.
点评 本题考查连接体的受力分析问题,熟练运用力的分解与合成即可求解,注意本题中整体法和隔离法的应用,另外,加速度也是矢量,分解时遵循平行四边形定则,难度适中.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
2. A、B两个离子同时从匀强磁场的直边界上的P、Q点分别以60°和30°(与边界的夹角)射入磁场,又同时分别从Q、P点穿出,如图所示.设边界上方的磁场范围足够大,下列说法中正确的是( )
A、B两个离子同时从匀强磁场的直边界上的P、Q点分别以60°和30°(与边界的夹角)射入磁场,又同时分别从Q、P点穿出,如图所示.设边界上方的磁场范围足够大,下列说法中正确的是( )
 A、B两个离子同时从匀强磁场的直边界上的P、Q点分别以60°和30°(与边界的夹角)射入磁场,又同时分别从Q、P点穿出,如图所示.设边界上方的磁场范围足够大,下列说法中正确的是( )
A、B两个离子同时从匀强磁场的直边界上的P、Q点分别以60°和30°(与边界的夹角)射入磁场,又同时分别从Q、P点穿出,如图所示.设边界上方的磁场范围足够大,下列说法中正确的是( )| A. | A为正离子,B的负离子 | B. | A、B两离子运动半径之比1:$\sqrt{3}$ | ||
| C. | A、B两离子速率之比为1:$\sqrt{3}$ | D. | A、B两离子的比荷之比为2:1 |
3. 如图所示,一简谐横波在t=0时的波形是图中实线,在t1=0.2s时的波形是图中虚线,P为介质中x=4m处的质点,则( )
如图所示,一简谐横波在t=0时的波形是图中实线,在t1=0.2s时的波形是图中虚线,P为介质中x=4m处的质点,则( )
 如图所示,一简谐横波在t=0时的波形是图中实线,在t1=0.2s时的波形是图中虚线,P为介质中x=4m处的质点,则( )
如图所示,一简谐横波在t=0时的波形是图中实线,在t1=0.2s时的波形是图中虚线,P为介质中x=4m处的质点,则( )| A. | 该波一定沿x轴正方向传播 | |
| B. | 该波的传播速度可能为5m/s | |
| C. | 从t=0开始,质点P经过0.2s沿x轴正方向运动1m | |
| D. | t=0.4s时,质点P的位置y=4cm |
20.关于热传递的叙述,正确的是( )
| A. | 在自然条件下,只要不违背能量的转化和守恒定律,热传递的过程总是可逆的 | |
| B. | 在自然条件下,热传递过程是可逆的 | |
| C. | 在自然条件下,热量也可以从低温物体传给高温物体 | |
| D. | 在自然条件下,热量不可能从低温物体传给高温物体 |
7.太阳系中某行星运行的轨道半径为R0,周期为T0.但天文学家在长期观测中发现,其实际运行的轨道总是存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离(行星仍然近似做匀速圆周运动).天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星.假设两行星的运行轨道在同一平面内,且绕行方向相同,则这颗未知行星运行轨道的半径R和周期T是(认为未知行星近似做匀速圆周运动)( )
| A. | T=$\frac{{{t}_{0}}^{2}}{{t}_{0}-{T}_{0}}$ | B. | T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0 | ||
| C. | R=R0$\root{3}{(\frac{{T}_{0}}{{t}_{0}-{T}_{0}})^{2}}$ | D. | R=R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ |
17.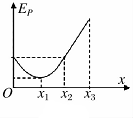 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3是直线段,则下列叙述不正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3是直线段,则下列叙述不正确的是( )
 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3是直线段,则下列叙述不正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3是直线段,则下列叙述不正确的是( )| A. | x1处电场强度为零 | |
| B. | x2~x3段是匀强电场 | |
| C. | x1、x2、x3处电势φ1、φ2、φ3的关系为φ1>φ2>φ3 | |
| D. | 粒子在0~x2段做匀变速运动,x2~x3段做匀速直线运动 |
4. 有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
 有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )| A. | a的向心加速度小于重力加速度g | B. | 在相同时间内b转过的弧长最长 | ||
| C. | c在4 h内转过的圆心角是$\frac{π}{3}$ | D. | d的运动周期有可能是20h |
1.一物体分别放在距离地面高为2R、3R处,受到地球的万有引力之比是( )
| A. | 9:4 | B. | 4:9 | C. | 16:9 | D. | 9:16 |
2. 如图,在斜面上木块A与B的接触面是水平的,绳子呈水平状态,两木块均保持静止.则关于木块A和木块B受力个数不可能的( )
如图,在斜面上木块A与B的接触面是水平的,绳子呈水平状态,两木块均保持静止.则关于木块A和木块B受力个数不可能的( )
 如图,在斜面上木块A与B的接触面是水平的,绳子呈水平状态,两木块均保持静止.则关于木块A和木块B受力个数不可能的( )
如图,在斜面上木块A与B的接触面是水平的,绳子呈水平状态,两木块均保持静止.则关于木块A和木块B受力个数不可能的( )| A. | 2个和4个 | B. | 3个和4个 | C. | 4个和4个 | D. | 4个和5个 |