题目内容
17.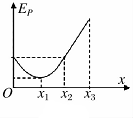 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3是直线段,则下列叙述不正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0~x2段是对称的曲线,x2~x3是直线段,则下列叙述不正确的是( )| A. | x1处电场强度为零 | |
| B. | x2~x3段是匀强电场 | |
| C. | x1、x2、x3处电势φ1、φ2、φ3的关系为φ1>φ2>φ3 | |
| D. | 粒子在0~x2段做匀变速运动,x2~x3段做匀速直线运动 |
分析 根据电势能与电势的关系:Ep=qφ,场强与电势的关系:E=$\frac{△φ}{△x}$,结合分析图象斜率与场强的关系,即可求得x1处的电场强度;根据能量守恒判断速度的变化;由Ep=qφ,分析电势的高低.由牛顿第二定律判断加速度的变化,即可分析粒子的运动性质.根据斜率读出场强的变化,由F=qE,分析电场力的变化
解答 解:A、根据电势能与电势的关系:Ep=qφ,场强与电势的关系:E=$\frac{△φ}{△x}$,得:E=$\frac{1}{q}•\frac{△{E}_{P}}{△x}$,由数学知识可知Ep-x图象切线的斜率等于$\frac{△{E}_{P}}{△x}$,x1处切线斜率为零,则x1处电场强度为零,故A正确
B、由图看出在0~x1段图象切线的斜率不断减小,由上式知场强减小,粒子所受的电场力减小,加速度减小,做非匀变速运动.x1~x2段图象切线的斜率不断增大,场强增大,粒子所受的电场力增大,做非匀变速运动.x2~x3段斜率不变,场强不变,即电场强度大小和方向均不变,是匀强电场,粒子所受的电场力不变,做匀变速直线运动,故B正确,D不正确;
C、根据电势能与电势的关系:Ep=qφ,粒子带负电,q<0,则知:电势能越大,粒子所在处的电势越低,所以有:φ1>φ2>φ3.故C正确
本题因选不正确的,故选:D
点评 解决本题的关键要分析图象斜率的物理意义,判断电势和场强的变化,再根据力学基本规律:牛顿第二定律进行分析电荷的运动情况

练习册系列答案
相关题目
5. 如图所示,真空中两点电荷+q和-q以相同角速度ω在水平面内绕O点顺时针转动,O点离+q较近,试判断O点的磁感应强度方向( )
如图所示,真空中两点电荷+q和-q以相同角速度ω在水平面内绕O点顺时针转动,O点离+q较近,试判断O点的磁感应强度方向( )
 如图所示,真空中两点电荷+q和-q以相同角速度ω在水平面内绕O点顺时针转动,O点离+q较近,试判断O点的磁感应强度方向( )
如图所示,真空中两点电荷+q和-q以相同角速度ω在水平面内绕O点顺时针转动,O点离+q较近,试判断O点的磁感应强度方向( )| A. | 方向垂直于纸面向外 | B. | 方向垂直于纸面向里 | ||
| C. | 为0 | D. | 无法确定 |
2. 如图,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的O点,以5m/s的速度水平抛出一个小球,则飞行一段时间后撞在斜面上时速度与水平方向夹角的正切值为(g=10m/s2)( )
如图,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的O点,以5m/s的速度水平抛出一个小球,则飞行一段时间后撞在斜面上时速度与水平方向夹角的正切值为(g=10m/s2)( )
 如图,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的O点,以5m/s的速度水平抛出一个小球,则飞行一段时间后撞在斜面上时速度与水平方向夹角的正切值为(g=10m/s2)( )
如图,斜面与水平面之间的夹角为45°,在斜面底端A点正上方高度为10m处的O点,以5m/s的速度水平抛出一个小球,则飞行一段时间后撞在斜面上时速度与水平方向夹角的正切值为(g=10m/s2)( )| A. | 2 | B. | 0.5 | C. | 1 | D. | $\sqrt{2}$ |
6. 嫦娥一号”探月卫星沿地月转移轨道到达月球,在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道Ⅰ绕月飞行,如右图所示.之后,卫星在P点经过几次“刹车制动”,最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.用T1、T2、T3分别表示卫星在椭圆轨道Ⅰ、Ⅱ和圆形轨道Ⅲ上运动的周期,用a1、a2、a3分别表示卫星沿三个轨道运动到P点的加速度,v1、v2、v3分别表示卫星沿三个轨道运动到P点的速度,用F1、F2、F3分别表示卫星沿三个轨道运动到P点时受到的万有引力,则下面关系式中正确的是( )
嫦娥一号”探月卫星沿地月转移轨道到达月球,在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道Ⅰ绕月飞行,如右图所示.之后,卫星在P点经过几次“刹车制动”,最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.用T1、T2、T3分别表示卫星在椭圆轨道Ⅰ、Ⅱ和圆形轨道Ⅲ上运动的周期,用a1、a2、a3分别表示卫星沿三个轨道运动到P点的加速度,v1、v2、v3分别表示卫星沿三个轨道运动到P点的速度,用F1、F2、F3分别表示卫星沿三个轨道运动到P点时受到的万有引力,则下面关系式中正确的是( )
 嫦娥一号”探月卫星沿地月转移轨道到达月球,在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道Ⅰ绕月飞行,如右图所示.之后,卫星在P点经过几次“刹车制动”,最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.用T1、T2、T3分别表示卫星在椭圆轨道Ⅰ、Ⅱ和圆形轨道Ⅲ上运动的周期,用a1、a2、a3分别表示卫星沿三个轨道运动到P点的加速度,v1、v2、v3分别表示卫星沿三个轨道运动到P点的速度,用F1、F2、F3分别表示卫星沿三个轨道运动到P点时受到的万有引力,则下面关系式中正确的是( )
嫦娥一号”探月卫星沿地月转移轨道到达月球,在距月球表面200km的P点进行第一次“刹车制动”后被月球捕获,进入椭圆轨道Ⅰ绕月飞行,如右图所示.之后,卫星在P点经过几次“刹车制动”,最终在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.用T1、T2、T3分别表示卫星在椭圆轨道Ⅰ、Ⅱ和圆形轨道Ⅲ上运动的周期,用a1、a2、a3分别表示卫星沿三个轨道运动到P点的加速度,v1、v2、v3分别表示卫星沿三个轨道运动到P点的速度,用F1、F2、F3分别表示卫星沿三个轨道运动到P点时受到的万有引力,则下面关系式中正确的是( )| A. | a1=a2=a3 | B. | v1>v2>v3 | C. | T1<T2<T3 | D. | F<1F2<F3 |
7. 如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A开始做自由落体运动,乙沿弦轨道从与圆心等高的B到达D,丙沿圆弧轨道从C点(很靠近D点)运动到D.忽略一切阻力,则正确的是( )
如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A开始做自由落体运动,乙沿弦轨道从与圆心等高的B到达D,丙沿圆弧轨道从C点(很靠近D点)运动到D.忽略一切阻力,则正确的是( )
 如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A开始做自由落体运动,乙沿弦轨道从与圆心等高的B到达D,丙沿圆弧轨道从C点(很靠近D点)运动到D.忽略一切阻力,则正确的是( )
如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A开始做自由落体运动,乙沿弦轨道从与圆心等高的B到达D,丙沿圆弧轨道从C点(很靠近D点)运动到D.忽略一切阻力,则正确的是( )| A. | 甲球最先到达D点,乙球最后到达D点 | |
| B. | 甲球最先到达D点,丙球最后到达D点 | |
| C. | 丙球最先到达D点,乙球最后到达D点 | |
| D. | 甲球最先到达D点,无法判断哪个球最后到达D点 |
 两质量均为2m的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B.求:
两质量均为2m的劈A和B,高度相同,放在光滑水平面上,A和B的倾斜面都是光滑曲面,曲面下端与水平面相切,如图所示,一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B.求: 测一节干电池的电动势E和内阻r.某同学设计了如图a所示的实验电路,已知电流表内阻与电源内阻相差不大.
测一节干电池的电动势E和内阻r.某同学设计了如图a所示的实验电路,已知电流表内阻与电源内阻相差不大. 如图所示,质量分别为m1=3kg和m2=1kg的两个物体A,B放在固定在地面上的光滑斜面上,斜面倾角为θ=37°,A,B之间的动摩擦因数为μ=0.2,已知最大静摩擦力等于滑动摩擦力,现对A施加一个水平力F使A,B保持相对静止一起沿斜面运动,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求力F的大小范围.
如图所示,质量分别为m1=3kg和m2=1kg的两个物体A,B放在固定在地面上的光滑斜面上,斜面倾角为θ=37°,A,B之间的动摩擦因数为μ=0.2,已知最大静摩擦力等于滑动摩擦力,现对A施加一个水平力F使A,B保持相对静止一起沿斜面运动,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求力F的大小范围.