题目内容
2013年12月14日21时11分,嫦娥三号成功着陆在月球西经19.5度、北纬44.1度的虹湾区域。如图所示是嫦娥三号奔月过程中某阶段运动的示意图,关闭动力的嫦娥三号在月球引力作用下沿圆轨道运动,在A处由圆轨道I变轨为椭圆轨道Ⅱ,以便更靠近月面。已知引力常量为G,圆轨道I的半径为r,周期为T.下列说法正确的是 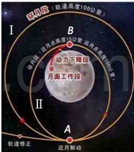
| A.嫦娥三号在A处由圆轨道Ⅰ变轨为椭圆轨道Ⅱ时,必须点火减速 |
| B.嫦娥三号沿椭圆轨道由A处飞向B处过程中,月球引力对其做负功 |
| C.根据题中条件可求出月球的平均密度 |
| D.根据题中条件可求出月球表面的重力加速度 |
A
解析试题分析:嫦娥三号在A处由圆轨道Ⅰ变轨为椭圆轨道Ⅱ时,做“近心运动”,提供的万有引力应大于所需的向心力,所以必须点火减速,故A正确;嫦娥三号沿椭圆轨道由A处飞向B处过程中,引力方向与速度方向夹角小于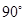 ,所以月球引力做正功,故B错误;嫦娥三号沿圆轨道绕月运行时,由月球的万有引力提供向心力,于是得:
,所以月球引力做正功,故B错误;嫦娥三号沿圆轨道绕月运行时,由月球的万有引力提供向心力,于是得: ,又因已知引力常量为G,圆轨道I的半径为r,周期为T,可计算出月球的质量,但月球的半径未知,其体积不可知,无法求出月球的平均密度,故C错误;在月球表面,货物受到的重力等于万有引力,即
,又因已知引力常量为G,圆轨道I的半径为r,周期为T,可计算出月球的质量,但月球的半径未知,其体积不可知,无法求出月球的平均密度,故C错误;在月球表面,货物受到的重力等于万有引力,即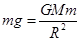 ,由于R未知,因此无法求出月球表面的重力加速度,故D错误。所以选A。
,由于R未知,因此无法求出月球表面的重力加速度,故D错误。所以选A。
考点:本题考查万有引力定律的应用,意在考查考生应用规律解决问题的能力。

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案甲、乙、丙三船在同一河流中渡河,船头和水流方向如图所示,已知三船在静水中的速度均大于水流速度v0,则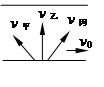
| A.甲船可能垂直到达对岸 | B.乙船可能垂直到达对岸 |
| C.丙船可能垂直到达对岸 | D.都不可能垂直到达对岸 |
在圆轨道运动的质量为m的人造地球卫星,它到地面的距离等于地球半径R,已知地面上的重力加速度为g,则( )
A.卫星运动的速度为 | B.卫星运动的周期为4p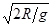 |
| C.卫星运动的加速度为g/2 | D.卫星的动能为mgR/2 |
(多选)有两颗人造地球卫星a、b在如图所示的轨道上做匀速圆周运动,下列说法中正确的是
| A.a的周期比b大 | B.a的向心加速度比b小 |
| C.a的向心力比b小 | D.a的角速度比b大 |
若某恒星系中所有天体的密度增大为原来的2倍,天体的直径和天体之间的距离不变,某行星绕该恒星做匀速圆周运动,则下述运行参量变化正确的是( )
| A.行星绕该恒星做匀速圆周运动的向心力变为原来的2倍 |
| B.行星绕该恒星做匀速圆周运动的线速度变为原来的4倍 |
| C.行星绕该恒星做匀速圆周运动的线速度变为原来的2倍 |
D.行星绕该恒星做匀速圆周运动的周期变为原来的 /2 /2 |
“嫦娥四号”月球飞船计划在2017年发射升空,现将它与“神舟十号”载人飞船进行类比分析。设月球、地球的质量分别为m1、m2,“嫦娥四号”与“神舟十号”轨道半径分别为 、
、 ,“神舟十号”环绕速度为v,环绕周期为T,则“嫦娥四号”在月球轨道上的环绕速度和环绕周期可表述为
,“神舟十号”环绕速度为v,环绕周期为T,则“嫦娥四号”在月球轨道上的环绕速度和环绕周期可表述为
A. , , | B. , , |
C. , , | D. , , |
我国2013年6月发射的“神州十号”飞船绕地球飞行的周期约为90分钟,取地球半径为6400km,地表重力加速度为g。设飞船绕地球做匀速圆周运动,则由以上数据无法估测
| A.飞船线速度的大小 | B.飞船的质量 |
| C.飞船轨道离地面的高度 | D.飞船的向心加速度大小 |
