题目内容
(8分)某行星的半径为R,它有一颗卫星,卫星绕它公转的轨道半径为r、公转周期为T.万有引力常量为G.求该行星的质量和密度。
 ,
,
解析试题分析:(1)万有引力提供卫星做半径为r的圆周运动,则:
 (4分)
(4分)
(2)该天体的体积为:
 (4分)
(4分)
考点:万有引力与航天

在一条宽200m的河中,水的流速v1=1m/s,一只小船要渡过河至少需要100s的时间。则下列判断正确的是:
| A.小船相对于静水的速度为2m/s |
| B.无论小船怎样渡河都无法到达正对岸 |
| C.若小船以最短时间渡河,到达对岸时,距正对岸100m |
| D.若小船航向(船头指向)与上游河岸成60°角,则小船渡河位移最短 |
下列关于万有引力的说法中,错误的是
| A.地面上自由下落的物体和天空中运行的月亮,都受到了万有引力的作用 |
| B.万有引力定律是牛顿在总结前人研究的基础上发现的 |
C. 中的G是比例常数,适用于任何两个物体之间,它没有单位 中的G是比例常数,适用于任何两个物体之间,它没有单位 |
| D.万有引力定律适用于自然界中任意两个物体之间 |
2013年12月14日21时11分,嫦娥三号成功着陆在月球西经19.5度、北纬44.1度的虹湾区域。如图所示是嫦娥三号奔月过程中某阶段运动的示意图,关闭动力的嫦娥三号在月球引力作用下沿圆轨道运动,在A处由圆轨道I变轨为椭圆轨道Ⅱ,以便更靠近月面。已知引力常量为G,圆轨道I的半径为r,周期为T.下列说法正确的是 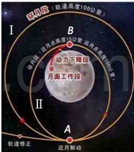
| A.嫦娥三号在A处由圆轨道Ⅰ变轨为椭圆轨道Ⅱ时,必须点火减速 |
| B.嫦娥三号沿椭圆轨道由A处飞向B处过程中,月球引力对其做负功 |
| C.根据题中条件可求出月球的平均密度 |
| D.根据题中条件可求出月球表面的重力加速度 |
探月热方兴未艾,我国研制的月球卫星 “嫦娥三号”于2013年12月14日成功登月。假设“嫦娥三号”在地球表面的重力为G1,重力加速度为g,在月球表面的重力为G2,地球与月球均视为均匀球体,其半径分别为R1、R2。则
A.月球表面的重力加速度为 |
B.月面附近卫星与地面附近卫星的速度之比为 |
C.月球与地球的质量之比为 |
D.“嫦娥三号”环绕月球面运动的周期为 |
2013年12月2日,我国探月工程“嫦娥三号”成功发射。“嫦娥三号”卫星实现了软着陆、无人探测及月夜生存三大创新。假设为了探测月球,载着登陆舱的探测飞船总质量为m1,在以月球中心为圆心、半径为r1的圆轨道上运动,周期为T1。登陆舱随后脱离飞船,变轨到离月球更近的半径为r2的圆轨道上运动,此时登陆舱的质量为m2。下列说法正确的是
A.月球的质量M= |
B.登陆舱在半径为r2轨道上运动的周期T2= |
C.登陆舱在半径为r1与半径为r2的轨道上运动的线速度之比为 |
D.月球表面的重力加速度 = = |
有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上随地球表面一起转动,b处于地面附近近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星,设地球自转周期为24h,所有卫星均视为匀速圆周运动,各卫星排列位置如图所示,则有( )
| A.a的向心加速度等于重力加速度g |
| B.c在4 h内转过的圆心角是π/6 |
| C.b在相同时间内转过的弧长最长 |
| D.d的运动周期有可能是23h |
 ,加速度为
,加速度为 ,运行速率为
,运行速率为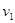 ;地球赤道上物体随地球自转的向心加速度为
;地球赤道上物体随地球自转的向心加速度为 ,运行速率为
,运行速率为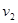 ,地球半径为
,地球半径为 .则
.则


