题目内容
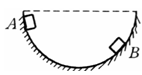
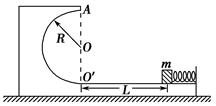
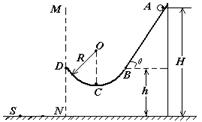
如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R =" 4" m的圆弧形轨道,且B点与D点在同一水平面上,在B点,轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处的一质量m=1kg的小球由静止滑下,经过B、C点后从D点斜抛出去,最后落在地面上的S点处时的速度大小vs = 8m/s,已知A点距地面的高度H = 10m,B点距地面的高度h ="5" m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2,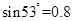 ,
,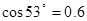 .问:
.问:
(1)小球经过B点的速度为多大?
(2)小球经过圆弧轨道最低处C点时对轨道的压力多大?
(3)小球从D点抛出后,受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.
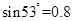 ,
,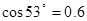 .问:
.问:
(1)小球经过B点的速度为多大?
(2)小球经过圆弧轨道最低处C点时对轨道的压力多大?
(3)小球从D点抛出后,受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.
(1)vB="10m/s." (2)N =" 43N." (3)W=-68J.
试题分析:(1)设小球经过B点时的速度大小为vB,由机械能守恒得:
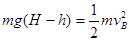 求得:vB=10m/s.
求得:vB=10m/s.(2)设小球经过C点时的速度为vC,对轨道的压力为N,则轨道对小球的压力N’=N,根据牛顿第二定律可得:
N’-mg =

由机械能守恒得:
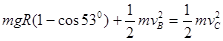
由以上两式及N’= N求得:N = 43N.
(3)设小球受到的阻力为f,到达S点的速度为vS,在此过程中阻力所做的功为W,易知vD= vB,由动能定理可得:
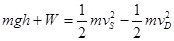 求得W=-68J.
求得W=-68J.点评:本题难度中等,利用机械能守恒定律求解问题时首先要判断机械能是否守恒,在圆周运动的最低点,通常根据合力提供向心力求解此时速度大小或支持力大小

练习册系列答案
相关题目