题目内容
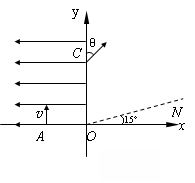
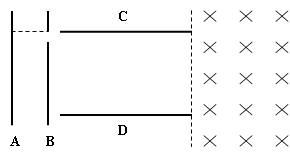
(12分)如图所示的直角坐标系中,第Ⅰ、Ⅳ象限内存在着垂直纸面向里的匀强磁场,在x=-2L与y轴之间第Ⅱ、Ⅲ象限内存在大小相等,方向相反的匀强电场,场强方向如图所示。在A(-2L,L)到C(-2L,0)的连线上连续分布着电荷量为+q、质量为m的粒子。从t=0时刻起,这些带电粒子依次以相同的速度v0沿x轴正方向射出。从A点射出的粒子刚好沿如图所示的运动轨迹(轨迹与x轴的交点为OC的中点)从y轴上A′(0,-L)沿x轴正方向进入磁场。不计粒子的重力及它们间的相互作用,不考虑粒子间的碰撞。 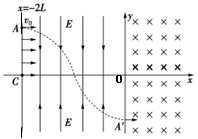
(1)求电场强度E的大小;
(2)若匀强磁场的磁感应强度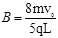 ,求从A′点进入磁场的粒子返回到直线x=-2L时的位置坐标;
,求从A′点进入磁场的粒子返回到直线x=-2L时的位置坐标;
(3)在AC间还有哪些位置的粒子,经过电场后也能沿x轴正方向进入磁场。
 (-2L,
(-2L, ) AC间y坐标为y=
) AC间y坐标为y= L(n=1,2,3,……)
L(n=1,2,3,……)
解析试题分析:(1)设粒子从A点射出到OC中点的时间为t,
根据类平抛运动规律则有:
x轴方向L=v0t 1分
y轴方向L=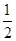 a(t)2 1分
a(t)2 1分
又qE=ma
解得:E= 1分
1分
(2)粒子在磁场中运动时,洛伦兹力提供向心力:qBv0= 1分
1分
解得:R= 1分
1分
可见粒子离开磁场时的位置坐标为(0,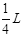 )
)
经分析可知,粒子在电场中有4段类平抛轨迹,则其返回到直线x=-2L时的位置坐标为(-2L, )
)
(3)设到C点距离为Δy处射出的粒子通过电场后也沿x轴正方向进入磁场,粒子第一次到达x轴用时Δt,水平位移为Δx,
则Δx=vΔt 1分
Δy=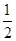 a(Δt2) 1分
a(Δt2) 1分
若满足2L=n·2Δx,则通过电场后能沿x轴正方向进入磁场 1分
解得:Δy=
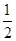 a(Δt2)=
a(Δt2)= L 2分
L 2分
即AC间y坐标为y= L(n=1,2,3,……)的粒子通过电场后能沿x轴正方向进入磁场。
L(n=1,2,3,……)的粒子通过电场后能沿x轴正方向进入磁场。
考点:本题考查带电粒子在混合场中的运动。

 阅读快车系列答案
阅读快车系列答案
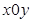 内,有一质量为
内,有一质量为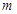 ,电荷量为
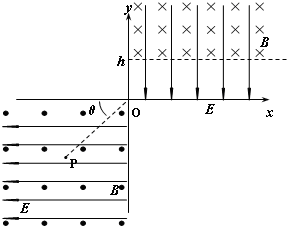
,电荷量为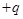 的粒子A从原点O沿y 轴正方向以初速度
的粒子A从原点O沿y 轴正方向以初速度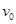 射出,粒子重力忽略不计,现要求该粒子能通过点P(a, -b),可通过在粒子运动的空间范围内加适当的“场”实现。
射出,粒子重力忽略不计,现要求该粒子能通过点P(a, -b),可通过在粒子运动的空间范围内加适当的“场”实现。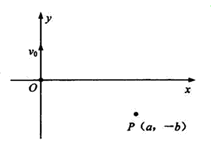
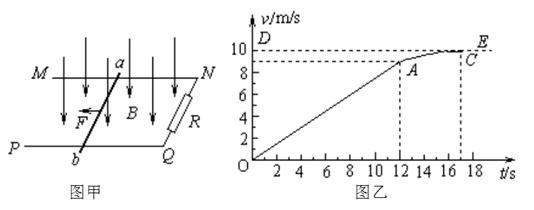

 的匀强磁场
的匀强磁场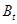 ,abcd的电阻值也为R,其他电阻不计.电阻两端又向右并联一个平行板电容器.在靠近M板处由静止释放一质量为m、电量为+q的带电粒子(不计重力),经过N板的小孔P进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为
,abcd的电阻值也为R,其他电阻不计.电阻两端又向右并联一个平行板电容器.在靠近M板处由静止释放一质量为m、电量为+q的带电粒子(不计重力),经过N板的小孔P进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为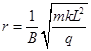 .求:
.求: