题目内容
(18分)如图所示,在直角坐标系xOy平面的第Ⅱ象限内有半径为R的圆O1分别与x轴、y轴相切于C(-R,0)、D(0,R) 两点,圆O1内存在垂直于xOy平面向外的匀强磁场,磁感应强度为B.与y轴负方向平行的匀强电场左边界与y轴重合,右边界交x轴于G点,一带正电的粒子A(重力不计)电荷量为q、质量为m,以某一速率垂直于x轴从C点射入磁场,经磁场偏转恰好从D点进入电场,最后从G点以与x轴正向夹角为45°的方向射出电场.求: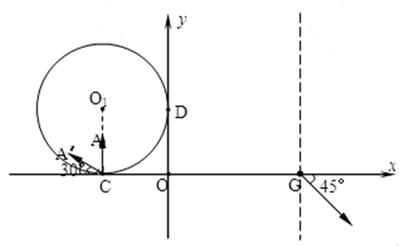
(1)OG之间的距离;
(2)该匀强电场的电场强度E;
(3)若另有一个与A的质量和电荷量相同、速率也相同的粒子A′,从C点沿与x轴负方向成30°角的方向射入磁场,则粒子A′再次回到x轴上某点时,该点的坐标值为多少?
(1)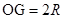 (2)
(2)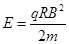 (3)(
(3)( ,0)
,0)
解析试题分析:(1)设粒子A速率为v0 ,其轨迹圆圆心在O点,故A运动至D点时速度与y轴垂直,粒子A从D至G作类平抛运动,令其加速度为a ,在电场中运行的时间为t
则有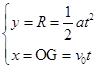 ① (2分)
① (2分)
和 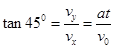 ②(2分)
②(2分)
联立①②解得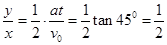
故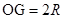 ③(1分)
③(1分)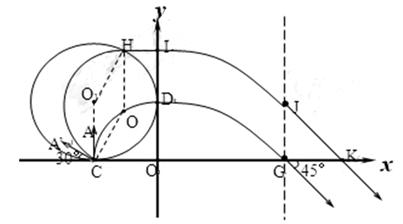
(2)粒子A的轨迹圆半径为R ,由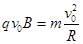 得
得  ④(2分)
④(2分)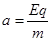 ⑤(1分)
⑤(1分)
联立①③⑤得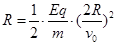 ⑥(2分)
⑥(2分)
解得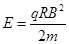 ⑦(1分)
⑦(1分)
(3)令粒子A’ 轨迹圆圆心为O’ ,因为∠O’ CA’ =90°,O’C=R,以 O’为圆心,R为半径做A’ 的轨迹圆交圆形磁场O1于H点,则四边形CO’ HO1为菱形,故O’ H∥y轴,粒子A’ 从磁场中出来交y轴于I点,HI⊥O’ H,所以粒子A’ 也是垂直于y轴进入电场的
令粒子A’ 从J点射出电场,交x轴于K点,因与粒子A在电场中的运动类似,
∠JKG=45°,GK=GJ。 (2分)
OI-JG=R又OI=R+Rcos30°解得JG=Rcos30°=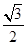 R (3分)
R (3分)
粒子A’再次回到x轴上的坐标为( ,0) (2分
,0) (2分
考点: 考查了牛顿第二定律与电磁学综合应用

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案如图所示,一人站在电梯中的体重计上,随电梯一起运动。下列各种情况中,体重计的示数最大的是
| A.电梯匀减速上升,加速度大小为 1.0 m/s2 |
| B.电梯匀减速下降,加速度大小为 1.0 m/s2 |
| C.电梯匀加速上升,加速度大小为 0.5 m/s2 |
| D.电梯匀加速下降,加速度大小为 0.5 m/s2 |
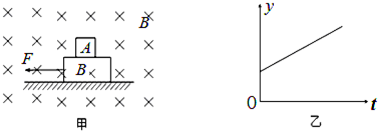
 的匀加速运动,上升了H高度,这一过程中bc间电阻r产生的焦耳热为Q,g为重力加速度,不计导轨电阻及感应电流间的相互作用。求:
的匀加速运动,上升了H高度,这一过程中bc间电阻r产生的焦耳热为Q,g为重力加速度,不计导轨电阻及感应电流间的相互作用。求:
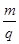 =4×10-10 kg/C的带正电粒子从x轴上的A点以初速度v0=2×107 m/s垂直x轴射入电场,OA=0.2 m,不计重力.求:
=4×10-10 kg/C的带正电粒子从x轴上的A点以初速度v0=2×107 m/s垂直x轴射入电场,OA=0.2 m,不计重力.求: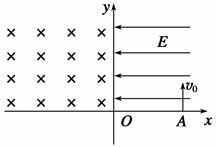
 ,
, )时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出。不计粒子的重力及粒子间相互作用力。求:
)时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出。不计粒子的重力及粒子间相互作用力。求:
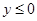 的区域内有方向垂直坐标平面的匀强磁场.一质量为m、电荷量为q的正粒子(不计重力),从P(
的区域内有方向垂直坐标平面的匀强磁场.一质量为m、电荷量为q的正粒子(不计重力),从P( )点由静止开始运动, 通过第二象限后经
)点由静止开始运动, 通过第二象限后经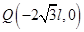 点再进入y≤0区域,并恰好经过坐标原点O.求
点再进入y≤0区域,并恰好经过坐标原点O.求
 .
.
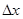
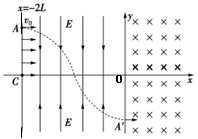
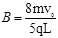 ,求从A′点进入磁场的粒子返回到直线x=-2L时的位置坐标;
,求从A′点进入磁场的粒子返回到直线x=-2L时的位置坐标;