题目内容
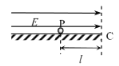
【题目】如图所示，相距L=5m的粗糙水平直轨道两端分别固定两个竖直挡板，距左侧挡板
=2m的O点处静止放置两个紧挨着的小滑块A、B，滑块之间装有少量炸药。炸药爆炸时，能将两滑块分开并保持在直轨道上沿水平方向运动。滑块A、B的质量均为m=1kg，与轨道间的动摩擦因数均为
=0.2。不计滑块与滑块、滑块与挡板间发生碰撞时的机械能损失，滑块可看作质点，重力加速度g取10m/s2。
(1)炸药爆炸瞬间，若有Q1=10J的能量转化成了两滑块的机械能，求滑块A最终离开出发点的距离；
(2)若两滑块A、B初始状态并不是静止的，当它们共同以v0=1m/s的速度向右经过O点时炸药爆炸，要使两滑块分开后能再次相遇，则爆炸中转化成机械能的最小值Q2是多少?
【答案】（1）1.5m；（2）19J
【解析】
(1)爆炸过程中，动量守恒，则有
根据能量守恒可得
解得
m/s
爆炸后二者减速运动，根据牛顿第二定律可得加速度均为
=2m/s2
爆炸后二者减速运动的位移
=2.5m
由于
，A会碰到挡板后原速率返回，在继续减速后停止
最终A停止时距离
点位移大小
=1.5m
(2)爆炸后A、B分开，可能有三种情况
情形①：A、B反向分开，A碰到挡板后反弹，在与B相遇
=10m
由以上可解得
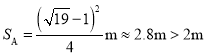
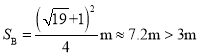
符合题意
解得
=19J
情形②：A、B反向分开，A未碰到挡板，B反弹后与A相遇
=6m
由以上可解得
与预设相矛盾
情形③：A、B同向分开，A慢B快，，B反弹后与A相遇
=6m
由以上方程联立后，无解
练习册系列答案
相关题目
