题目内容
11.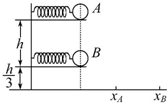 (多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )
(多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )| A. | 竖直支架应向上移动 | B. | 竖直支架应向下移动 | ||
| C. | 竖直支架移动的距离为h | D. | 竖直支架移动的距离为$\frac{4h}{15}$ |
分析 平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动,根据A、B的高度比求出运动的时间比,从而根据水平射程比得出初速度之比,再通过子弹的水平位移相等,求出时间比,从而求出高度比,从而得出竖直支架移动的距离.
解答 解:开始hA=$\frac{4}{3}h$,hB=$\frac{1}{3}h$,根据H=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2H}{g}}$,则$\frac{{t}_{A}}{{t}_{B}}=\frac{2}{1}$,
因为$\frac{{x}_{A}}{{x}_{B}}=\frac{1}{2}$,则$\frac{{v}_{A}}{{v}_{B}}=\frac{1}{4}$.
调整高度后,水平位移相等,则运动时间比变为$\frac{{t}_{A}}{{t}_{B}}=\frac{4}{1}$,
则竖直位移之比$\frac{{h}_{A}′}{{h}_{B}′}=\frac{16}{1}$,
设A的高度为H,有$\frac{H}{H-h}=\frac{16}{1}$,解得H=$\frac{16}{15}h$,
则支架下降的距离△h=$\frac{4}{3}h-\frac{16}{15}h=\frac{4}{15}h$.故B、D正确,A、C错误.
故选:BD.
点评 解决本题的关键知道平抛运动的时间由高度决定,时间和初速度共同决定水平位移.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
19.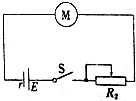 如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则( )
如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则( )
 如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则( )
如图所示,电源电动势为E,内阻为r,电动机M的线圈电阻为R1.闭合开关S,电动机开始转动,稳定后电路中的电流为I,滑动变阻器接入电路的电阻为R2.则( )| A. | 电源的输出功率为IE-I2r | B. | 电动机两端的电压U=IR1 | ||
| C. | 电源的效率η=$\frac{{R}_{1}+{R}_{2}}{{R}_{1}+{R}_{2}+r}$×100% | D. | 电动机的机械功率P=IE-I2(R1+R2+r) |
6.关于功和功率.以下说法正确的是( )
| A. | 滑动摩擦力对物体一定做负功 | |
| B. | 静摩擦力对物体可能做正功 | |
| C. | 功率是描述力对物体做功多少的物理量 | |
| D. | 某个力对物体做功越多,它的功率就一定大 |
16.某人以一定的速率垂直河岸将船向对岸划去,河水各处的流速均相同,关于它过河所需时间,发生的位移与水速的关系是( )
| A. | 水速小时,位移小,时间不变 | B. | 水速大时,位移大,时间长 | ||
| C. | 水速大时,位移小,时间不变 | D. | 位移,时间与水速无关 |
20.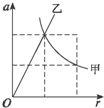 甲、乙两质点做匀速圆周运动,如图所示为向心加速度随半径变化的图线,甲为双曲线,乙为过原点的直线,则( )
甲、乙两质点做匀速圆周运动,如图所示为向心加速度随半径变化的图线,甲为双曲线,乙为过原点的直线,则( )
 甲、乙两质点做匀速圆周运动,如图所示为向心加速度随半径变化的图线,甲为双曲线,乙为过原点的直线,则( )
甲、乙两质点做匀速圆周运动,如图所示为向心加速度随半径变化的图线,甲为双曲线,乙为过原点的直线,则( )| A. | 甲的线速度不变 | B. | 甲的角速度不变 | C. | 乙的线速度不变 | D. | 乙的角速度不变 |
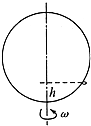 一个小圆环套在置于竖直面内半径为r的大圆环上,并能沿大圆环无摩擦地滑动,当大圆环绕一个穿过其中心的竖直轴转动时,小圆环便相对静止在距大圆环最低点上方h处,如图所示,试求:大圆环转动的角速度ω.
一个小圆环套在置于竖直面内半径为r的大圆环上,并能沿大圆环无摩擦地滑动,当大圆环绕一个穿过其中心的竖直轴转动时,小圆环便相对静止在距大圆环最低点上方h处,如图所示,试求:大圆环转动的角速度ω.
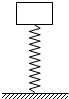 如图所示,一质量为m的物体放在竖直的弹簧上,并令其上下作简谐运动.振动过程中物体对弹簧的最大压力为1.5mg,则求
如图所示,一质量为m的物体放在竖直的弹簧上,并令其上下作简谐运动.振动过程中物体对弹簧的最大压力为1.5mg,则求 半径为R的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点.在O的正上方有一个可视为质点的小球以初速度v水平抛出,半径OA的方向恰好与v的方向相同,如图所示.若小球与圆盘只碰一次,且落在A点,重力加速度为g,
半径为R的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点.在O的正上方有一个可视为质点的小球以初速度v水平抛出,半径OA的方向恰好与v的方向相同,如图所示.若小球与圆盘只碰一次,且落在A点,重力加速度为g,