题目内容
2.如图光滑水平导轨AB的左端有一压缩的弹簧,弹簧左端固定,右端前放一个质量为m=1kg的物块(可视为质点),物块与弹簧不粘连,B点与水平传送带的左端刚好平齐接触,传送带的长度BC的长为L=6m,CD为光滑的水平轨道,C点与传送带的右端刚好平齐接触,DE是竖直放置的半径为R=0.4m的光滑半圆轨道,DE与CD相切于D点.已知物块与传送带间的动摩擦因数μ=0.2,取g=10m/s2.
(1)若第一次释放弹簧时传送带静止不动,物块离开弹簧后滑上传送带刚好能到达C点,求弹簧释放前储存的弹性势能Ep;
(2)若第二次释放弹簧时传送带沿逆时针方向以恒定速度v=2m/s匀速转动.物块离开弹簧,滑上传送带能够通过C点,并经过圆弧轨道DE,从其最高点E飞出,最终落在CD上距D点的距离为x=1.2m处(CD长大于1.2m),求物块通过D点时受到的支持力大小;
(3)满足(2)条件时,求物块通过传送带的过程中产生的热能.
分析 (1)弹簧弹性的势能完全转化为木块的动能,木块通过传送带时滑动摩擦力做的功等于木块动能的变化,据此计算可得;
(2)滑块从E点开始做平抛运动,根据平抛运动规律求得木块经过E点时的速度,再根据机械能守恒定律可求得D点的速度,由牛顿第二定律求得木块在D点受到的压力;
(3)求出木块经过传送带时与传送带间的相对位移,根据Q=fL求得因摩擦产生的热能.
解答 解:(1)滑块经过传送带时,摩擦力做的功等于滑块动能的变化,故有:
$-μmgL=0-\frac{1}{2}m{v}^{2}$
可知滑块释放时的动能为:
$\frac{1}{2}m{v}^{2}=μmgL=0.2×1×10×6J=12J$
弹簧释放时弹簧的弹性势能完全转化为木块的动能,所以滑块刚好到达传送带C点时弹簧储存的弹性势能为:12J;
(2)小滑块离开E点做平抛运动,由平抛知识有:
水平方向:x=vEt
竖直方向:$y=2R=\frac{1}{2}g{t}^{2}$
由此可得,滑块在E点的速度为:${v}_{E}=\frac{x}{t}=\frac{x}{\sqrt{\frac{4R}{g}}}=\frac{1.2}{\sqrt{\frac{4×0.4}{10}}}m/s=3m/s$
根据动能定理有:滑块从D到E的过程中只有重力做功:
$-mg•2R=\frac{1}{2}m{v}_{E}^{2}-\frac{1}{2}m{v}_{D}^{2}$
代入数据解得:滑块经过D点时的速度为:vD=5m/s
由向心力公式可得:
FN=mg+m$\frac{{v}_{D}^{2}}{R}$=10+1×$\frac{25}{0.4}$=72.5N
(3)滑块经过传送带时只有阻力做功,根据动能定理有:
$-μmgL=\frac{1}{2}m{v}_{D}^{2}-\frac{1}{2}m{v}_{B}^{2}$
代入数据可解得:vB=7m/s
因为滑块做匀减速运动,故有:
L=$\frac{{v}_{B}+{v}_{D}}{2}$t,可得滑块在传送带上运动的时间为:t=$\frac{6}{\frac{5+7}{2}}s=1s$
由此可知滑块在传送带上滑动时,滑块相对于传送带的位移为:x=L+vt=6+2×1m=8m
所以滑块因摩擦产生的热量为:Q=μmgx=0.2×1×10×8J=16J
答:(1)若释放弹簧,物块离开弹簧,滑上传送带刚好能到达C点,弹簧储存的弹性势能Ep为12J;
(2)物块通过D点时受到的支持力大小72.5N;
(3)满足(2)条件时,求物块通过传送带的过程中产生的热能为16J.
点评 本题是传送带与平抛运动的结合,关键是能掌握物体在传送带上做匀减速运动,能根据平抛运动规律求解平抛运动问题,以及摩擦生热由两物体间的相对位移决定.

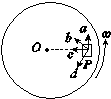 如图所示,物块P置于水平转盘上随转盘一起运动,且与圆盘相对静止,图中c沿半径指向圆心,a与c垂直,下列说法正确的是( )
如图所示,物块P置于水平转盘上随转盘一起运动,且与圆盘相对静止,图中c沿半径指向圆心,a与c垂直,下列说法正确的是( )| A. | 当转盘匀速转动时,P受摩擦力方向为c方向 | |
| B. | 当转盘加速转动时,P受摩擦力方向可能为b方向 | |
| C. | 当转盘加速转动时,P受摩擦力方向可能为a方向 | |
| D. | 当转盘减速转动时,P受摩擦力方向可能为d方向 |
| A. | 知道阿伏加德罗常数、气体的摩尔质量和密度,可估算出气体分子大小 | |
| B. | 已知气体分子间的作用力表现为引力,若气体膨胀则气体分子势能增加 | |
| C. | 分子间距离越大,分子势能越大,分子间距离越小,分子势能越小 | |
| D. | 在热传导中,如果两个系统达到热平衡,则它们具有相同的温度 |
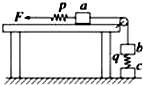 三个质量均为1kg的相同木块a、b、c和两个劲度系数均为500N/m的相同轻弹簧p、q用轻绳连接,如图所示,其中a放在光滑水平桌面上.开始时p弹簧处于原长,木块都处于静止状态,轻绳处于拉直状态.现用水平力F缓慢地向左拉p弹簧的左端,直到c木块刚好离开水平地面为止,g取10m/s2.该过程p弹簧的左端向左移动的距离是( )
三个质量均为1kg的相同木块a、b、c和两个劲度系数均为500N/m的相同轻弹簧p、q用轻绳连接,如图所示,其中a放在光滑水平桌面上.开始时p弹簧处于原长,木块都处于静止状态,轻绳处于拉直状态.现用水平力F缓慢地向左拉p弹簧的左端,直到c木块刚好离开水平地面为止,g取10m/s2.该过程p弹簧的左端向左移动的距离是( )| A. | 4 cm | B. | 6 cm | C. | 8 cm | D. | 10 cm |
| A. | 4倍 | B. | 8倍 | C. | 16倍 | D. | 64倍 |
 人用手托着质量为m的小苹果,从静止开始沿水平方向运动,前进距离l后,速度为v(小苹果与手始终相对静止),小苹果与手掌之间的动摩擦因数为μ,则下列说法正确的是( )
人用手托着质量为m的小苹果,从静止开始沿水平方向运动,前进距离l后,速度为v(小苹果与手始终相对静止),小苹果与手掌之间的动摩擦因数为μ,则下列说法正确的是( )| A. | 手对小苹果的作用力方向始终竖直向上 | |
| B. | 小苹果所受摩擦力大小为μmg | |
| C. | 手对小苹果做的功为$\frac{1}{2}$mv2 | |
| D. | 速度为v时,小苹果重力的瞬时功率为mgv |
| A. | 物体(质量不变)的速度发生变化,则动能一定发生变化 | |
| B. | 物体(质量不变)的动能发生变化,则速度一定发生变化 | |
| C. | 物体(质量不变)的动能不发生变化,物体所受合力一定是零 | |
| D. | 物体(质量不变)在合力作用下做匀变速直线运动,则动能在这段过程中的变化量一定不为零 |
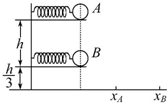 (多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )
(多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )| A. | 竖直支架应向上移动 | B. | 竖直支架应向下移动 | ||
| C. | 竖直支架移动的距离为h | D. | 竖直支架移动的距离为$\frac{4h}{15}$ |