题目内容
1.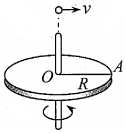 半径为R的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点.在O的正上方有一个可视为质点的小球以初速度v水平抛出,半径OA的方向恰好与v的方向相同,如图所示.若小球与圆盘只碰一次,且落在A点,重力加速度为g,
半径为R的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点.在O的正上方有一个可视为质点的小球以初速度v水平抛出,半径OA的方向恰好与v的方向相同,如图所示.若小球与圆盘只碰一次,且落在A点,重力加速度为g,(1)小球抛出时距O的高度是多少?
(2)圆盘转动的角速度大小?
分析 小球做平抛运动,小球在水平方向上做匀速直线运动,在竖直方向做自由落体运动,根据水平位移求出运动的时间,根据竖直方向求出高度.圆盘转动的时间和小球平抛运动的时间相等,在这段时间内,圆盘转动n圈.
解答 解:(1)取小球为研究对象,设从抛出到落到A点时间为t.有
$\left.\begin{array}{l}{R=vt}\end{array}\right.$,
$h=\frac{1}{2}g{t}^{2}$,
得 $t=\frac{R}{v}$,$h=\frac{{g{R^2}}}{{2{v^2}}}$
(2)由题意可知,在小球下落时间内,圆盘转过的角度是2nπ(n=1、2、3…).
则 $ω=\frac{2nπ}{t}=\frac{2nπv}{R}$(n=1、2、3…).
答:(1)小球抛出时距O的高度是$\frac{g{R}^{2}}{2{v}^{2}}$;
(2)圆盘转动的角速度大小为$\frac{2nπv}{R}$(n=1、2、3…).
点评 解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,以及知道圆盘转动的周期性.

练习册系列答案
相关题目
11.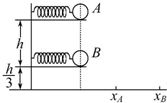 (多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )
(多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )
 (多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )
(多选)在一个竖直的支架上固定着两个水平的弹簧枪A和B,弹簧枪A、B在同一竖直平面内,如图所示,A比B高h,弹簧枪B的出口距水平面高$\frac{h}{3}$,弹簧枪A、B射出的子弹的水平射程之比为xA:xB=1:2.设弹簧枪A、B的高度差h不变,且射出子弹的初速度不变,要使两个弹簧枪射出的子弹落到水平面上的同一点,则( )| A. | 竖直支架应向上移动 | B. | 竖直支架应向下移动 | ||
| C. | 竖直支架移动的距离为h | D. | 竖直支架移动的距离为$\frac{4h}{15}$ |
9.下列关于匀速圆周运动的说法中,正确的是( )
| A. | 是线速度不变的运动 | B. | 是相对圆心位移不变的运动 | ||
| C. | 是角速度不断变化的运动 | D. | 是角速度不变的运动 |
16.关于地球同步卫星的说法,正确的是( )
| A. | 轨道半径越大,运行速率也越大 | |
| B. | 地球同步卫星的运行速率大于7.9km/s | |
| C. | 地球同步卫星有可能定点于北京地区的上空 | |
| D. | 所有的地球同步卫星在同一圆周轨道上 |
6.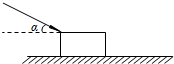 放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )
放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )
 放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )
放在水平地面上的物块,受到一个与水平方向成α角斜向下方的力F的作用,物块在水平地面静止,如图所示.如果保持力F的大小不变,而使力F与水平方向的夹角α增大,那么,地面受到的压力N和物块受到的摩擦力f的变化情况是( )| A. | N变小,f变大 | B. | N变小,f变小 | C. | N变大,f变小 | D. | N变大,f不变 |
10.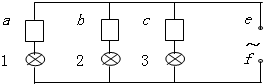 如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )
如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )
 如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )
如图所示,在e、f间接上交流电源,保持电压最大值不变,使其频率增大,发现各灯的亮度变化情况是:灯1变暗,灯2变亮,灯3不变.则黑箱a、b、c中所接元件可能是( )| A. | a为电阻,b为电容器,c为电感线圈 | B. | a为电阻,b为电感线圈,c为电容器 | ||
| C. | a为电容器,b为电感线圈,c为电阻 | D. | a为电感线圈,b为电容器,c为电阻 |
7.下列物理量的单位中,属于国际单位制中的基本单位的是( )
| A. | 牛顿 | B. | 秒 | C. | 焦耳 | D. | 瓦 |
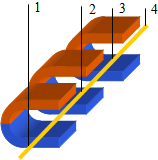 在“探究影响安培力大小的因素”的实验中,如图所示,三块相同的蹄形磁体并列放置,可以认为磁场是均匀的.将一根直导线用导电轻绳悬挂在磁体的两极间,有电流通过时轻绳将摆动一个角度,通过这个角度可以比较安培力的大小.
在“探究影响安培力大小的因素”的实验中,如图所示,三块相同的蹄形磁体并列放置,可以认为磁场是均匀的.将一根直导线用导电轻绳悬挂在磁体的两极间,有电流通过时轻绳将摆动一个角度,通过这个角度可以比较安培力的大小.