题目内容
已知地球同步卫星的轨道半径约为地球半径的6.6倍．一飞行器绕地球做匀速圆周运动的周期为3小时。若地球半径为R，则该飞行器绕地心飞行的轨道半径最接近（ ）
| A．0.83R | B．1.7R | C．1.9R | D．3.3R |
B
解析试题分析：将开普勒第三定律用到地球系统，所有的卫星的轨道半径的三次方与公转周期的平方的比值都相等，故：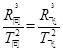
，解得：
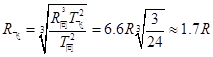故选：B．
考点：开普勒第三定律.
阶梯计算系列答案太空被称为是21世纪技术革命的摇篮．摆脱地球引力，在更“纯净”的环境中探求物质的本质，拨开大气层的遮盖，更直接地探索宇宙的奥秘，一直是科学家们梦寐以求的机会．“神州号” 两次载人飞船的成功发射与回收给我国航天界带来足够的信心，我国提出了载人飞船 太空实验室 空间站的三部曲构想．某宇航员要与轨道空间站对接，飞船为了追上轨道空间站
| A．只能从较低轨道上加速 |
| B．只能从较高轨道上加速 |
| C．只能从空间站同一高度的轨道上加速 |
| D．无论在什么轨道上，只要加速都行 |
我国“嫦娥二号”卫星于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空，并获得了圆满成功．发射的大致过程是：先将卫星送入绕地椭圆轨道，再点火加速运动至月球附近被月球“俘获”而进入较大的绕月椭圆轨道，又经三次点火制动“刹车”后进入近月圆轨道，在近月圆轨道上绕月运行的周期是118分钟．又知月球表面的重力加速度是地球表面重力加速度（g=10m/s2）的1/6．则（ ）
| A．仅凭上述信息及数据能算出月球的半径 |
| B．仅凭上述信息及数据能算出月球上的第一宇宙速度 |
| C．仅凭上述信息及数据能算出月球的质量和密度 |
| D．卫星沿绕地椭圆轨道运行时，卫星上的仪器处于完全失重状态 |
倍，则太阳与地球的质量之比为：（ ）
已知地球质量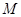为
，半径为
，自转周期为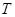
，地球同步卫星质量为
，引力常量为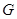
.有关同步卫星，下列表述正确的是（ ）
A．卫星距离地面的高度为 |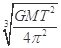
| B．卫星的运行速度大于第一宇宙速度 |
C．卫星运行时受到的向心力大小为 |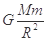
| D．卫星运行的向心加速度小于地球表面的重力加速度 |
要使可视为质点的两物体间万有引力减小到原来的1/4，下列办法不可采用的是
| A．使两物体的质量各减小一半，距离不变 |
| B．使其中一个物体的质量减小到原来的1/4，距离不变 |
| C．使两物体间的距离增为原来的2倍，质量不变 |
| D．使两物体间的距离和质量都减为原来的1/4 |
“嫦娥一号”是我国首次发射的探月卫星，它在距月球表面高度为200km的圆形轨道上运行，运行周期为127分钟。已知引力常量G=6.67×10-11N·m2/kg2，月球半径约为1.74×103km。利用以上数据估算月球的质量约为（ ）
| A．8.1×1010kg | B．7.4×1013 kg |
| C．5.4×1019 kg | D．7.4×1022 kg |
某研究小组用天文望远镜对一颗行星进行观测，发现该行星有一颗卫星，卫星在行星的表面附近绕行，并测得其周期为T，已知引力常量为G，根据这些数据可以估算出（ ）
| A．行星的质量 | B．行星的半径 |
| C．行星的平均密度 | D．行星表面的重力加速度 |
如图所示，发射地球同步卫星时，先将卫星发射至近地圆轨1然后经点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步圆轨道3，轨道1和2相切于Q点，轨道2和3相切于P点，设卫星在1轨道和3轨道正常运行的速度和加速度分别为v1、v3和a1、a3，在2轨道经过P点时的速度和加速度为v2和a2，且当卫星分别在1、2、3轨道上正常运行时周期分别为T1、T2、T3，以下说法正确的是( )
| A．v1 > v3> v2 | B．v1> v2 > v3 |
| C．a1 >a2 > a3 | D．T1 < T2 < T3 |