题目内容
某研究小组用天文望远镜对一颗行星进行观测,发现该行星有一颗卫星,卫星在行星的表面附近绕行,并测得其周期为T,已知引力常量为G,根据这些数据可以估算出( )
| A.行星的质量 | B.行星的半径 |
| C.行星的平均密度 | D.行星表面的重力加速度 |
C
解析试题分析:卫星绕行星运动时,引力充当向心力,则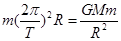 或
或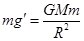 ,无法求出M、R、gˊ,但可通过
,无法求出M、R、gˊ,但可通过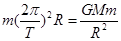 变形得
变形得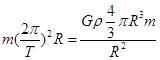 可求出
可求出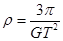 ,则C正确
,则C正确
考点:本题考查万有引力充当向心力、万有引力在天体运动中应用。

已知地球同步卫星的轨道半径约为地球半径的6.6倍.一飞行器绕地球做匀速圆周运动的周期为3小时。若地球半径为R,则该飞行器绕地心飞行的轨道半径最接近( )
| A.0.83R | B.1.7R | C.1.9R | D.3.3R |
9月底美国的UARS卫星坠落不是第一次航天器坠落地球事件,自1957年人类进入太空时代以来,曾经有600多个航天器落入大气层。人类迄今为止发射了5000多颗航天器,除了那些深空探测、跑远了的卫星(比如“旅行者”“先驱者”等探测器),基本上最后的命运都是落叶归根,落回地球。有的体积、质量较小,就被大气层烧干净了。有的体积、质量较大,烧不干净,就要落回地球。美国的UARS卫星在缓慢落入大气层的过程中( )
| A.线速度越来越小 | B.角速度越来越小 |
| C.周期越来越小 | D.向心加速度越来越小 |
“天宫一号”和“神舟十号”交会对接成功,标志着我国在对接技术上迈出了重要一步,用M代表“神舟十号”,N代表“天宫一号”,它们对接前做圆周运动的情形如图所示,则( )
| A.M的运行速度小于N的运行速度 |
| B.M的向心加速度大于N的向心加速度 |
| C.M的运行周期大于N的运行周期 |
| D.M适度加速可与N对接 |
下表是火星和地球部分数据对照表,把火星和地球视为匀质理想球体,它们绕太阳的运动近似看作匀速圆周运动,从表中数据可以分析得出不正确的是( )
| | 质量 (kg) | 公转周期 (d天) | 自转周期 (h小时) | 近似公转轨道半径(m) | 星球半径 (m) |
| 火星 | 6.421×1023 | 686.98 | 24.62 | 2.28×1011 | 3.395×106 |
| 地球 | 5.976×1024 | 365.26 | 23.93 | 1.50×1011 | 6.378×106 |
B.地球公转动能较大
C.火星的第一宇宙速度较大
D.火星两极处地表重力加速度较小
我国发射的探月卫星有一类为绕月极地卫星。利用该卫星可对月球进行成像探测。如图所示,设卫星在绕月极地轨道上做圆周运动时距月球表面的高度为H,绕行周期为TM; 月球绕地球公转的周期为TE,公转轨道半径为R0;地球半径为RE,月球半径为RM. 忽略地球引力、太阳引力对绕月卫星的影响,则下列说法正确的是
A.月球与地球的质量之比为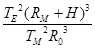 |
B.若光速为C,信号从卫星传输到地面所用时间为 |
C.由开普勒第三定律可得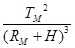 = =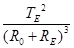 |
D.由开普勒第三定律可得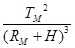 = =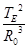 |
如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )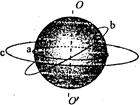
| A.a、b、c做匀速圆周运动的向心加速度大小关系为ab>ac>aa |
| B.b与c相比,b的发射速度大,运行速度vb大 |
| C.a、b、c做匀速圆周运动的线速度大小关系为va=vb>vc |
| D.a、b、c做匀速圆周运动的周期关系为Ta>Tc>Tb |
若已知月球绕地球运动可近似看做匀速圆周运动,并且已知月球绕地球运动的轨道半径r,它绕地球运动的周期T,万有引力常量是G,由此可以知道
A.月球的质量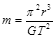 | B.地球的质量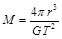 |
C.月球的平均密度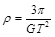 | D.地球的平均密度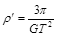 |
 ;某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R.则下列判断中正确的是
;某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R.则下列判断中正确的是


 分别为卫星Ⅰ与卫星Ⅱ的质量
分别为卫星Ⅰ与卫星Ⅱ的质量