��Ŀ����
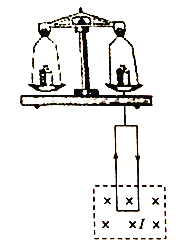
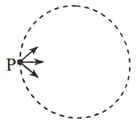
����Ŀ����ͼ��������ʾ��Բ�������ڴ���һ��ֱ��ֽ�����ǿ�ų���PΪ�ų��߽��ϵ�һ�㣬������ͬ�Ĵ�����������ͬ�����ʾ���P�㣬��ֽ�����ز�ͬ�ķ�������ų���������������ٶ�Ϊ![]() ����Щ�����ڴų��߽�ij����ֲ�������֮һԲ���ϣ������������ٶ�Ϊ
����Щ�����ڴų��߽�ij����ֲ�������֮һԲ���ϣ������������ٶ�Ϊ![]() ����Ӧ�ij����ֲ�������֮һԲ���ϣ�������������������֮�������ã����ٶ�Ϊv1���������ٶ�Ϊv2�������ٶ�֮��
����Ӧ�ij����ֲ�������֮һԲ���ϣ�������������������֮�������ã����ٶ�Ϊv1���������ٶ�Ϊv2�������ٶ�֮��![]() .
.
���𰸡�![]()
������������������ҵ��Ӵų��߽�����������DZ���Ĺؼ������ڴ�P�����������������Բ���˶��İ뾶��ͬ��������ͬ�����Կ�����һ����Բ��Բ����һ����P��ת�����Ӷ���ȷ���ڴų�Բ�ཻ�����Ӷ�����������֪�����е�����
��Բ������ų��İ뾶Ϊr�����ٶȴ�СΪ![]() ʱ����P���������������ų�ʱ��ų��߽����Զ����ΪMʱ����ͼ��ʾ��
ʱ����P���������������ų�ʱ��ų��߽����Զ����ΪMʱ����ͼ��ʾ��
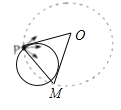
������֪![]() ���ɼ��ι�ϵ�ù켣Բ�뾶Ϊ
���ɼ��ι�ϵ�ù켣Բ�뾶Ϊ![]() ����P���������������ų�ʱ��ų��߽����Զ����ΪN����ͼ��ʾ��
����P���������������ų�ʱ��ų��߽����Զ����ΪN����ͼ��ʾ��
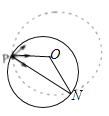
������֪![]() ���ɼ��ι�ϵ�ù켣Բ�İ뾶Ϊ
���ɼ��ι�ϵ�ù켣Բ�İ뾶Ϊ![]()
�������������䵱��������֪�� ![]()
�ã� ![]()
����![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ