题目内容
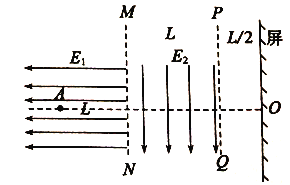
【题目】如图所示，固定的粗细可忽略的竖直杆MN及固定的半圆形凹槽。凹槽的最右端到竖直杆的距离d=2.4m。凹槽虚线所在的直径水平，凹槽半径R=
m。体积可忽略的小求A与体积可忽略的圆环B用不可伸长的轻绳相连，圈环套在竖直杆上。用外力使小球A静止于凹槽的最右端，此时轻绳伸直，轻绳与坚直杆的夹角θ=37°，忽略一切聚擦阻力，由静上释放小球A，已知小球A的质量
，圆环B的质量mB=1kg。试求：当小球A运动到凹槽的最低点时，其速度的大小vA=？
【答案】
【解析】当小球A运动到凹槽底端时，AB之间的距离减小量为
；
因原来AB=
，此时AB=3m；
由几何关系可得末位置轻绳与竖直杆之间的夹角α=53°·
则小环上升的高度h=
=1.4m
由机械能守恒定律可得：mAgR=mBgh+
mAvA2+mBvB2·
vAcos45°=vBcosα·
vA=0.84m/s
练习册系列答案
相关题目
