题目内容
【题目】(1)两个行星质量分别为m1和m2，绕太阳运行的轨道半径分别是r1和r2，则它们与太阳间的万有引力之比为________．它们的公转周期之比________．
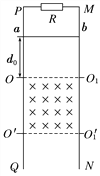
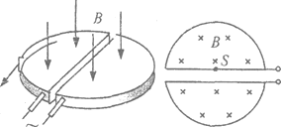
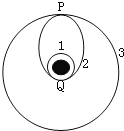
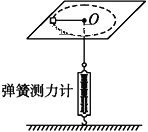
(2)航天器绕地球做匀速圆周运动时处于完全失重状态，物体对支持面几乎没有压力，所以在这种环境中已经无法用天平称量物体的质量。假设某同学在这种环境中设计了如图所示的装置(图中O为光滑小孔)来间接测量物体的质量:给待测物体一个初速度，使它在桌面上做匀速圆周运动。设航天器中具有测量长度和时间的基本测量工具。
1)实验时需要测量的物理量是：____________。（说明各物理量对应的字母）
2)待测物体质量的表达式为m= _______(用所测物理量字母表示)。
【答案】
弹簧测力计示数F、圆周运动的半径R、圆周运动的周期T 
【解析】
（1）万有引力定律
，可知引力大小与它们的质量成正比，与间距的平方成反比，
则它们与太阳之间的万有引力之比是m1r22：m2r12。
由万有引力充当向心力知
知：
，所以它们公转的周期之比是。
（2）物体做匀速圆周运动的向心力由拉力提供，根据牛顿第二定律有：
，可知要测出物体的质量，则需测量弹簧秤的示数F，圆周运动的半径R以及物体做圆周运动的周期T。根据，得
。
【题目】以下是一位同学做“探究形变与弹力的关系”的实验。
（1）下列的实验步骤是这位同学准备完成的，请你帮这位同学按操作的先后顺序，用字母排列出来是： 。
A．以弹簧伸长量为横坐标，以弹力为纵坐标，描出各组数据（x，F）对应的点，并用平滑的曲线连结起来。 |
B．记下弹簧不挂钩码时，其下端在刻度尺上的刻度L0 |
C．将铁架台固定于桌子上，并将弹簧的一端系于横梁上，在弹簧附近竖直固定一刻度尺 |
D．依次在弹簧下端挂上1个、2个、3个、4个……钩码，并分别记下钩码静止时，弹簧下端所对应的刻度并记录在表格内，然后取下钩码 |
E、以弹簧伸长量为自变量，写出弹力与弹簧伸长量的关系式.
F、解释函数表达式中常数的物理意义.
（2）下表是这位同学探究弹力大小与弹簧伸长量之间的关系所测的几组数据：
弹力（F/N） | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
弹簧原来长度（L0/cm） | 15 | 15 | 15 | 15 | 15 |
弹簧后来长度（L/cm） | 16.0 | 17.1 | 18.0 | 18.9 | 20 |
弹簧伸长量（x/cm） | 1.0 | 2.1 | 3.0 | 3.9 | 5.0 |
据上表的数据在右下图的坐标中作出F-x图线。
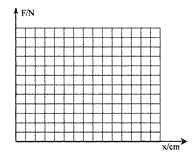
②写出曲线的函数表达式。（x用cm作单位）：
③函数表达式中常数的物理意义：
