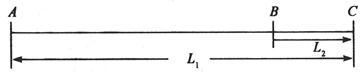题目内容
如图所示,倾角θ=30°的足够长光滑斜面下端与一光滑水平面相接,连接处用一光滑小圆弧过渡,斜面上距水平面高度分别为h1=5m和h2=0.2m的两点上,各静置一小滑块A和B。某时刻由静止开始释放滑块A,经过一段时间t后,再由静止开始释放滑块B。g取10m/s2,求:
(1)为了保证A、B两滑块不会在斜面上相碰,t最长不能超过多少?
(2)若滑块A从斜面上h1高度处自由下滑的同时,滑块B受到恒定外力作用从P点以加速度a=2m/s2由静止开始向左运动,滑块A经多长时间追上滑块B?
1.6s 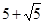
解析试题分析:(1)A、B两物块释放以后会做加速度相同的匀加速直线运动,当释放时间大于他们运动到斜面低端所需的时间差时,就会在斜面上相碰。(2)B物块做初速度为零,加速度不同的匀变速直线运动,A物体开始做匀变速直线运动,到达水平面后做匀速直线运动,当他们相遇时,在水平面上通过的位移相等,由此可列方程求解。
(1)设两滑块沿斜面下滑的加速度为a1,据牛顿第二定律有:
mgsinθ=ma1①(2分)
设A、B两滑块滑到斜面底端所用时间分别为t1、t2,由运动学方程有: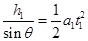 ②(1分)
②(1分)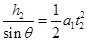 ③(1分)
③(1分)
要A、B两滑块不在斜面上相碰,t≤t1-t2 ④(2分)
由①~④式并代入已知数据可得:t≤1.6s (2分)
(2)设A物块从开始运动到与物块B相碰历时t0时间,两物块在水平面上的位移相等: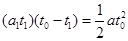 ⑤(2分)
⑤(2分)
由①⑤式并带入数据可解得: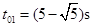 ,
, 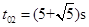 (2分)
(2分)
所以A物块从开始运动到与物块B相碰历时(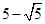 )s (1分)
)s (1分)
考点:牛顿第二定律,追击问题

练习册系列答案
相关题目
如图所示,一匹马拉着车在公路上加速前进。关于马拉车的力与车拉马的力,下列说法正确的是( )
| A.由于马车加速前进,马拉车的力大于车拉马的力 |
| B.只有马车匀速前进,马拉车的力才等于车拉马的力 |
| C.马拉车的力与车拉马的力是一对平衡力,大小始终相等 |
| D.马拉车的力与车拉马的力是一对相互作用力,大小始终相等 |
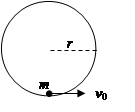
 如图所示,在光滑水平地面上有一固定的挡板,挡板上固定一个轻弹簧。现有一质量
如图所示,在光滑水平地面上有一固定的挡板,挡板上固定一个轻弹簧。现有一质量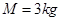 ,长
,长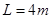 的小车
的小车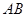 (其中
(其中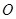 为小车的中点,
为小车的中点,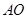 部分粗糙,
部分粗糙,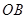 部分光滑),一质量为
部分光滑),一质量为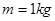 的小物块(可视为质点),放在车的最左端,车和小物块一起以
的小物块(可视为质点),放在车的最左端,车和小物块一起以 的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车
的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车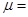 0.3,重力加速度
0.3,重力加速度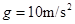 。求:
。求: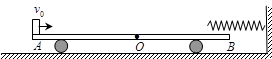
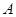 端多远。
端多远。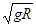 .在PO的右侧空间存在方向竖直向下的匀强电场。一质量为m、电荷 量 为+q的小物体从圆弧顶点A由静止开始沿轨道下滑,恰好运动到C端后返回。物体与传送带间的动摩擦因数为
.在PO的右侧空间存在方向竖直向下的匀强电场。一质量为m、电荷 量 为+q的小物体从圆弧顶点A由静止开始沿轨道下滑,恰好运动到C端后返回。物体与传送带间的动摩擦因数为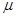 ,不计物体经过轨道与传送带连接处P时的机械能损失,重力加速度为g。
,不计物体经过轨道与传送带连接处P时的机械能损失,重力加速度为g。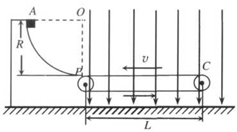
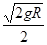 ,试 求 物体 在传送带上运动的时间t。
,试 求 物体 在传送带上运动的时间t。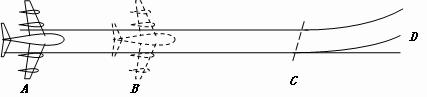
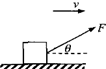
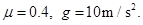 某选手作用在瓶子上的水平推力F="20" N,瓶子沿AC做直线运动,假设瓶子可视为质点,该选手要想游戏获得成功,试问:
某选手作用在瓶子上的水平推力F="20" N,瓶子沿AC做直线运动,假设瓶子可视为质点,该选手要想游戏获得成功,试问: