题目内容
（12分）航天宇航员在月球表面完成了如下实验：如图所示，在月球表面固定一竖直光滑圆形轨道，在轨道内的最低点，放一可视为质点的小球，当给小球水平初速度v0时，小球刚好能在竖直面内做完整的圆周运动。已知圆形轨道半径为r，月球的半径为R。求：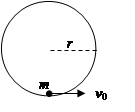
（1）月球表面的重力加速度g；
（2）轨道半径为2R的环月卫星周期T。
（1）g=v02/5r （2）4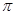
解析试题分析：（1）设小球的质量为m，因小球恰好能完成圆周运动，
小球在最高点有：mg=mv2/r
最低点到最高点的过程有-mg.2r=mv2/2-mv20/2
联立这两式得：g=v02/5r
（2）设月球的质量为M，卫星质量为m’
对卫星有GMm’/4R2=m’4 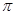22R/T2
对小球有GMm/R2=mg
联立③④⑤得 T="2"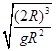 
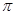=4
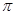
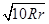
考点：本题考查圆周运动规律和机械能守恒定律以及万有引力定律的应用。
练习册系列答案
相关题目
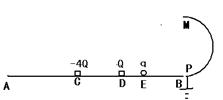
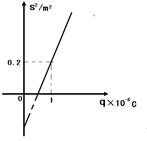
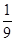×10－6C，如图所示，将小球B缓缓拉离竖直位置，当绳与竖直方向的夹角为60°时，将其由静止释放，小球B将在竖直面内做圆周运动．已知释放瞬间绳刚好张紧，但无张力．静电力常量
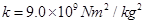，g取10m/s2。求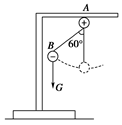
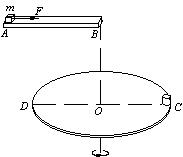
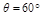，小球质量为m=0.5kg，D点与小孔A的水平距离s=2m，g取10m/s2。求：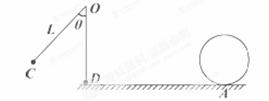
。（g="10" m/s2）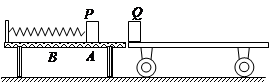
.在PO的右侧空间存在方向竖直向下的匀强电场。一质量为m、电荷量 为+q的小物体从圆弧顶点A由静止开始沿轨 道下滑，恰好运动到C端后返回。物体与传送 带间的动摩擦因数为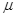
，不计物体经过轨道与传 送带连接处P时的机械能损失,重力加速度为g
，试求物体在传送带上运动的时间t。