Question

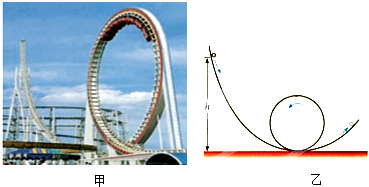
【题目】如图所示，abc是光滑的轨道，其中ab是水平的，bc为与ab相切的位于竖直平面内的半圆，半径R=0.30m．质量m=0.20kg的小球A静止在轨道上，另一质量M=0.60kg、速度V0=5.5m/s的小球B与小球A正碰．已知相碰后小球A经过半圆的最高点c落到轨道上距b点为，l=4 R处，重力加速度g=10m/s2 ， 求：

（1）碰撞结束后，小球A和B的速度的大小．
（2）试论证小球B是否能沿着半圆轨道到达c点．

Answer 1

【答案】
（1）解：分别以v1和v2表示小球A和B碰后的速度，v1′表示小球A在半圆最高点的速度，t表示小球A从离开半圆到落在轨道上经过的时间，则有：

依据平抛运动竖直方向的分运动特点知：

gt2=2R

对于小球碰后到最高点过程，应用动能定理得：

﹣mg×2R= mv′2﹣

对于B与A的碰撞过程应用水平方向动量守恒得：

Mv0=mv1+Mv2

联立以上各式解得： =3.5m/s

=6m/s

（2）解：假定B球刚好能沿半圆轨道上升到C点，则在C点时，轨道对它的作用力为零，以vc表示它在C处的速度，vb表示它在B处的相应速度，由牛顿第二定律和机械能守恒定律得：Mg=

解得： =3.9m/s＞v2

故B球不能达到半圆轨道最高点C

【解析】（1）根据平抛运动的规律，求出A球在C点的速度，根据机械能守恒定律求出A球碰后的速度，根据动量守恒定律求出B球碰后的速度．（2）根据机械能守恒定律求出B球到底最高点的速度，再根据牛顿第二定律求出最高点的最小速度，然后进行比较，判断能否到达最高点