题目内容
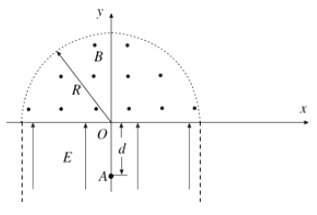
【题目】如图所示，在x轴下方的区域内存在沿y轴正向的匀强电场，电场强度为E。在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场，磁场的方向垂直于xy平面并指向纸面外，磁感应强度为B。y轴下方的A点与O点的距离为d，一质量为m、电荷量为q的带正电粒子从A点由静止释放，经电场加速后从O点射入磁场。(不计粒子的重力)
(1)求粒子在磁场中运动的轨道半径r；
(2)要使粒子进入磁场之后不再经过x轴，电场强度需大于或等于某个值E0，求E0；
(3)若电场强度E等于第(2)问E0的
，求粒子经过x轴时的位置。
【答案】(1)
(2)
(3)
【解析】
试题分析；（1）粒子在电场中加速，由动能定理得
qEd＝
mv2① （2分）
粒子进入磁场后做圆周运动，有
qvB＝m
② （2分）
解得粒子在磁场中运动的半径
r＝
③ （2分）
（2）粒子之后恰好不再经过x轴，则离开磁场时的速度方向与x轴平行，运动情况如图①，
可得R＝
r ④ （3分） 由以上各式解得 E0＝（3分）
（3）将E＝
E0代入可得磁场中运动的轨道半径 r＝
⑥ （2分）
粒子运动情况如图②，图中的角度α、β满足
cosα＝
＝
（2分） 即α＝30° ⑦ （2分） β＝2α＝60° ⑧ （2分）
粒子经过x轴时的位置坐标为
x＝r＋
⑨ （2分）
解得x＝
R. ⑩ （2分）
练习册系列答案
相关题目
