题目内容
【题目】如图，一个质量为m=2kg的小物块静置于足够长的斜面底端。现对其施加一个沿斜面向上、大小为F=25N的恒力，3s后将F撤去，此时物块速度达到15m/s。设物块运动过程中所受摩擦力的大小不变，取g=10m/s2。求：
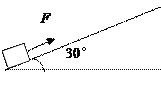
（1）物块在斜面上运动离斜面底端的最远距离；
（2）物块在斜面上运动的总时间（结果可用根式表示）。
【答案】（1）37.5m（2）(5+
)s
【解析】（1）物块的加速度为：
，
由牛顿第二定律得：F-f-mgsinθ=ma1
解得：f=5N；
撤去拉力后，物块继续上滑，由牛顿第二定律得：f+mgsinθ=ma2，
解得：a2=7.5m/s2，
撤力前物块向上滑行的距离：
撤去拉力后物块向上滑行的距离：
物块在斜面上运动离斜面底端的最远距离：x=x1+x2=22.5+15=37.5m；
（2）撤力后物块上滑的时间：
物块沿斜面向下滑动过程，由牛顿第二定律得：mgsinθ-f=ma3，
解得：a3=2.5m/s2，
由x＝
a3t32可知，滑块的运动时间：
滑块在斜面上运动的总时间：t＝t1+t2+t3＝5+（s）≈10.48s；
练习册系列答案
相关题目
