题目内容
9. 水平地面上有质量分别为m和4m的物块A和B,两者与地面间的动摩擦因数均为μ,细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示,初始时,A、B均处于静止状态,并且绳水平拉直,若物块A在水平向右的拉力F作用下向右移动了距离s,重力加速度大小为g,求:
水平地面上有质量分别为m和4m的物块A和B,两者与地面间的动摩擦因数均为μ,细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示,初始时,A、B均处于静止状态,并且绳水平拉直,若物块A在水平向右的拉力F作用下向右移动了距离s,重力加速度大小为g,求:(1)物块A的加速度大小;
(2)物块B的速度大小.
分析 (1)分别对AB受力分析,根据牛顿第二定律进行列式,结合两个物体加速度关系,联立可求得物体A和B的加速度.
(2)根据B的位移和加速度,由速度位移公式求物块B的速度大小.
解答 解:(1)设物块A、B的加速度大小分别为aA、aB,绳中的张力为T.由牛顿第二定律
对A有:F-μmg-T=maA
对B有:2T-4μmg=4maB
由A和B的位移关系得:
aA=2aB
联立解得:aA=$\frac{F-3μmg}{2m}$,aB=$\frac{F-3μmg}{4m}$
(2)物块A移动了距离s时,物块B移动的距离为:
sB=$\frac{1}{2}$s
由${v}_{B}^{2}$=2aBsB,解得:
vB=$\sqrt{\frac{(F-3μmg)s}{4m}}$
答:(1)物块A的加速度大小是$\frac{F-3μmg}{2m}$;
(2)物块B的速度大小是$\sqrt{\frac{(F-3μmg)s}{4m}}$.
点评 本题考查牛顿第二定律以及运动学公式的应用,关键要抓住两个物体之间的关系,如加速度关系、位移关系,要注意明确研究对象的选取,正确受力分析,再根据牛顿第二定律和运动学公式研究.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.一水平放置的平行板电容器的两极板间距为d,极板分别与电池两极相连,上极板中心有一小孔(小孔对电场的影响可忽略不计).小孔正上方$\frac{d}{2}$处的P点有一带电粒子,该粒子从静止开始下落,经过小孔进入电容器,并在下极板处(未与极板接触)返回.若将下极板向上平移$\frac{d}{4}$,则从P点开始下落的相同粒子将( )
| A. | 打到下极板上 | B. | 在下极板处返回 | ||
| C. | 在距上极板$\frac{2}{5}$d处返回 | D. | 在距上极板$\frac{d}{2}$处返回 |
14.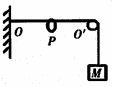 如图所示,一根不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于点O′的固定光滑轴悬挂一质量为M的物体;轻绳OO′段水平,长度为L;绳子上套一可沿绳滑动的轻环P.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为( )
如图所示,一根不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于点O′的固定光滑轴悬挂一质量为M的物体;轻绳OO′段水平,长度为L;绳子上套一可沿绳滑动的轻环P.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为( )
 如图所示,一根不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于点O′的固定光滑轴悬挂一质量为M的物体;轻绳OO′段水平,长度为L;绳子上套一可沿绳滑动的轻环P.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为( )
如图所示,一根不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于点O′的固定光滑轴悬挂一质量为M的物体;轻绳OO′段水平,长度为L;绳子上套一可沿绳滑动的轻环P.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为( )| A. | $\sqrt{2}$M | B. | $\sqrt{3}$M | C. | $\frac{\sqrt{2}}{2}$M | D. | $\frac{\sqrt{3}}{2}$M |
18.将一个力分解为两个分力,合力与分力的关系,下说法中错误的是( )
| A. | 合力的大小一定等于两个分力大小之和 | |
| B. | 合力的大小可能比每一个分力都大,也可能比每一个分力都小 | |
| C. | 合力的大小可能小于每一个分力的大小 | |
| D. | 合力的大小一定比一个分力大,比另一个分力小 |
19.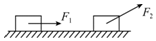 用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )
用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )
 用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )
用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )| A. | 两次合外力的功相同 | B. | 第一次合外力的功较大 | ||
| C. | 两次拉力的功相同 | D. | 第二次拉力的功较大 |
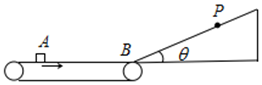 如图所示,足够长的浅色传送带以速度v0=8m/s顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量m=1kg的墨色小滑块从距离B点s0=10m的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为μ1=0.4,斜面倾角θ=37°,斜面足够长,滑块与斜面的动摩擦因数μ2=0.45,重力加速度g=10m/s2,sin37°=0.6cos37°=0.8,求:
如图所示,足够长的浅色传送带以速度v0=8m/s顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量m=1kg的墨色小滑块从距离B点s0=10m的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为μ1=0.4,斜面倾角θ=37°,斜面足够长,滑块与斜面的动摩擦因数μ2=0.45,重力加速度g=10m/s2,sin37°=0.6cos37°=0.8,求: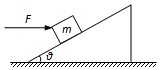 如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2) 如图所示,物体的质量m=4kg,放在摩擦系数为0.25粗糙的水平面上.现在用一大小为40N力F作用在物体上,力F与水平方向的夹角为37°,使物体水平向右做匀加速直线运动运动,重力加速度g=10m/s2,已知sin37°=0.6,cos37°=0.8
如图所示,物体的质量m=4kg,放在摩擦系数为0.25粗糙的水平面上.现在用一大小为40N力F作用在物体上,力F与水平方向的夹角为37°,使物体水平向右做匀加速直线运动运动,重力加速度g=10m/s2,已知sin37°=0.6,cos37°=0.8