题目内容
14.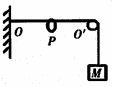 如图所示,一根不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于点O′的固定光滑轴悬挂一质量为M的物体;轻绳OO′段水平,长度为L;绳子上套一可沿绳滑动的轻环P.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为( )
如图所示,一根不可伸长的光滑轻绳,其左端固定于O点,右端跨过位于点O′的固定光滑轴悬挂一质量为M的物体;轻绳OO′段水平,长度为L;绳子上套一可沿绳滑动的轻环P.现在轻环上悬挂一钩码,平衡后,物体上升L.则钩码的质量为( )| A. | $\sqrt{2}$M | B. | $\sqrt{3}$M | C. | $\frac{\sqrt{2}}{2}$M | D. | $\frac{\sqrt{3}}{2}$M |
分析 由几何关系求出环两边绳子的夹角,然后根据平行四边形定则可求得钩码的重力,再根据G=mg可求得钩码的质量.
解答  解:由题意可知,重新平衡后,绳子形状如下图:由于OO'长为L,物体上升高度L,说明绳子在左侧总长度为L,则左右两边均为L,如图所示,则可知,sinθ=$\frac{1}{2}$,故绳子与竖直方向夹角为30°,则环两边绳子的夹角为60°,则根据平行四边形定则,环两边绳子拉力的合力为F=2Mgcos30°=$\sqrt{3}$Mg,根据平衡条件,则钩码重力为$\sqrt{3}$Mg,则可知钩码的质量为$\sqrt{3}$M.故B正确ACD错误.
解:由题意可知,重新平衡后,绳子形状如下图:由于OO'长为L,物体上升高度L,说明绳子在左侧总长度为L,则左右两边均为L,如图所示,则可知,sinθ=$\frac{1}{2}$,故绳子与竖直方向夹角为30°,则环两边绳子的夹角为60°,则根据平行四边形定则,环两边绳子拉力的合力为F=2Mgcos30°=$\sqrt{3}$Mg,根据平衡条件,则钩码重力为$\sqrt{3}$Mg,则可知钩码的质量为$\sqrt{3}$M.故B正确ACD错误.
故选:B.
点评 本题的关键在于能够对线圈进行受力分析,利用平衡状态条件解决问题.要注意明确力的计算离不开几何关系和三角函数的应用.

练习册系列答案
相关题目
16.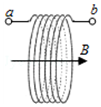 如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )
如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )
 如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )
如图为无线电充电技术中使用的受电线圈示意图,线圈匝数为n,面积为S,若在t1到t2时间内,匀强磁场平行于线圈轴线向右穿过线圈,其磁感应强度大小由B1均匀增加到B2,则该段时间线圈两端a和b之间的电势差φa-φb是( )| A. | 数值恒为 $\frac{nS({B}_{2}-{B}_{1})}{{t}_{2}-{t}_{1}}$ | |
| B. | φa-φb大于零 | |
| C. | 数值从0均匀变化到$\frac{nS({B}_{2}-{B}_{1})}{{t}_{2}-{t}_{1}}$ | |
| D. | φa-φb小于零 |
5. 如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )
如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )
 如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )
如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )| A. | 物块C对A的作用力大小为mg | |
| B. | 小球B的加速度方向向左,大小为$\frac{g}{tanθ}$ | |
| C. | 地面对A的支持力大小为(M+m)g | |
| D. | 地面与A之间的滑动摩擦因数为tanθ |
19.下列说法正确的是( )
| A. | 电动势公式E=$\frac{W}{q}$中的W与电势差公式U=$\frac{W}{q}$中的W是一样的,都是静电力做的功 | |
| B. | 电动势E是由电源本身决定的,跟电源的体积和外电路均无关 | |
| C. | 为防止颠簸造成损坏,灵敏电流表在运输时常用导线将接线柱连在一起,这样指针的摆动幅度会大大减小 | |
| D. | 金属探测器可用于食品生产,防止细小的砂石颗粒混入食品中 |
6. 一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )
一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )
 一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )
一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速地放在传送带的最左端,木炭包在传送带上将会留下一段黑色的径迹.下列说法中正确的是( )| A. | 木炭包的质量越大,径迹的长度越短 | |
| B. | 黑色的径迹将出现在木炭包的右侧 | |
| C. | 传送带运动的速度越大,径迹的长度越短 | |
| D. | 木炭包与传送带间动摩擦因数越大,径迹的长度越短 |
3. 如图所示,甲、乙两图中闭合线圈均匀速从Ⅰ位置经过Ⅱ位置移至Ⅲ位置,情况分别为:甲图中,线圈垂直于S极与N极连线套于条形磁体外部,中心在条形磁体的轴线上,Ⅱ位置为条形磁体的中央位置:乙图中,线圈在一通电长直导线上方,Ⅱ位置为直导线的正上方.请分析以上两种情况中,线圈在通过Ⅱ位置时.下列说法正确的是( )
如图所示,甲、乙两图中闭合线圈均匀速从Ⅰ位置经过Ⅱ位置移至Ⅲ位置,情况分别为:甲图中,线圈垂直于S极与N极连线套于条形磁体外部,中心在条形磁体的轴线上,Ⅱ位置为条形磁体的中央位置:乙图中,线圈在一通电长直导线上方,Ⅱ位置为直导线的正上方.请分析以上两种情况中,线圈在通过Ⅱ位置时.下列说法正确的是( )
 如图所示,甲、乙两图中闭合线圈均匀速从Ⅰ位置经过Ⅱ位置移至Ⅲ位置,情况分别为:甲图中,线圈垂直于S极与N极连线套于条形磁体外部,中心在条形磁体的轴线上,Ⅱ位置为条形磁体的中央位置:乙图中,线圈在一通电长直导线上方,Ⅱ位置为直导线的正上方.请分析以上两种情况中,线圈在通过Ⅱ位置时.下列说法正确的是( )
如图所示,甲、乙两图中闭合线圈均匀速从Ⅰ位置经过Ⅱ位置移至Ⅲ位置,情况分别为:甲图中,线圈垂直于S极与N极连线套于条形磁体外部,中心在条形磁体的轴线上,Ⅱ位置为条形磁体的中央位置:乙图中,线圈在一通电长直导线上方,Ⅱ位置为直导线的正上方.请分析以上两种情况中,线圈在通过Ⅱ位置时.下列说法正确的是( )| A. | 甲乙瞬时电流都不为零 | B. | 甲乙瞬时电流均为零 | ||
| C. | 甲瞬时电流为零 | D. | 乙瞬时电流为零 |
2.2015年5月4日河南省襄城高中举行了18岁成人仪式,会上放飞了象征着欢乐祥和的气球.假定2(1)班学生小明放飞气球时,天空中无风,地球周围空气密度不随高度变化,不考虑运动过程中气球体积的变化,但空气阻力与速度成正比.则气球在运动过程中( )
| A. | 气球在空中上升过程中只受到重力和浮力两个力作用 | |
| B. | 气球一直做加速直线运动 | |
| C. | 气球达到最大速度前,速度变化越来越慢 | |
| D. | 气球在上升过程中,先加速后减速,最终匀速 |
 有两个用特殊材料做成的两个物体A和B,质量都为m,它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=k(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g)
有两个用特殊材料做成的两个物体A和B,质量都为m,它们之间存在一种相互作用,这个作用力F与它们间的距离x的关系为F=k(x0-x),其中k、x0为已知常数,当两者间距离x<x0时,这个作用表现为斥力,当x>x0时,这个作用表现为引力,当x=x0时,作用力为零.现将物体B固定在水平地面上,再将A移到B的正上方,最终A能静止于B的正上方的某处,试求:(已知重力加速度大小为g) 水平地面上有质量分别为m和4m的物块A和B,两者与地面间的动摩擦因数均为μ,细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示,初始时,A、B均处于静止状态,并且绳水平拉直,若物块A在水平向右的拉力F作用下向右移动了距离s,重力加速度大小为g,求:
水平地面上有质量分别为m和4m的物块A和B,两者与地面间的动摩擦因数均为μ,细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示,初始时,A、B均处于静止状态,并且绳水平拉直,若物块A在水平向右的拉力F作用下向右移动了距离s,重力加速度大小为g,求: