题目内容
20.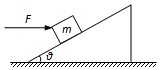 如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)求:(1)物体和斜面体间的动摩擦因数;
(2)若不改变F的方向,但大小变为F′,使物体在斜面上匀速下滑,求此时F′的大小.
分析 (1)物体匀速下滑,根据受力分析,利用共点力平衡求得摩擦因数
(2)物体匀速下滑,根据受力分析,利用共点力平衡求得推力
解答 解:(1)对物体,受到重力、水平推力、斜面的支持力和沿斜面向下的滑动摩擦力四个力的作用而做匀速直线运动,将力沿平行于斜面和垂直于斜面正交分解,可得在平行于斜面的方向上,有:Fcosθ-mgsinθ-μN=0
在垂直于斜面的方向上,有:N-Fsinθ-mgcosθ=0
代入数据解得:μ=0.5
(2)根据共点力平衡可知mgsinθ=F′cosθ+μ(mgcosθ+F′sinθ)
解得$F′=\frac{40}{11}$N
答:(1)物体和斜面体间的动摩擦因数为0.5;
(2)若不改变F的方向,但大小变为F′,使物体在斜面上匀速下滑,此时F′的大小为$\frac{40}{11}$N
点评 本题两次平衡问题,运用平衡条件分析研究两次,实质上滑动摩擦力大小没有变化,但方向相反.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )
如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )
 如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )
如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )| A. | a比b后着地 | B. | a与c可能同时着地 | ||
| C. | a和b可能同时着地 | D. | a、b、c着地时速度大小可能相等 |
15. 如图所示,竖直固定的光滑杆上套有一个质量为m的小球A,不可伸长的轻质细绳通过固定在天花板上、大小可忽略的定滑轮O,连接小球A和小球B,虚线OC水平,此时连接小球A的细绳与水平的夹角为60°,小球A恰能保持静止.现在小球B的下端再挂一个物块,使得小球A可从图示位置上升并恰好能到达C处,不计摩擦和空气阻力,重力加速度为g.则( )
如图所示,竖直固定的光滑杆上套有一个质量为m的小球A,不可伸长的轻质细绳通过固定在天花板上、大小可忽略的定滑轮O,连接小球A和小球B,虚线OC水平,此时连接小球A的细绳与水平的夹角为60°,小球A恰能保持静止.现在小球B的下端再挂一个物块,使得小球A可从图示位置上升并恰好能到达C处,不计摩擦和空气阻力,重力加速度为g.则( )
 如图所示,竖直固定的光滑杆上套有一个质量为m的小球A,不可伸长的轻质细绳通过固定在天花板上、大小可忽略的定滑轮O,连接小球A和小球B,虚线OC水平,此时连接小球A的细绳与水平的夹角为60°,小球A恰能保持静止.现在小球B的下端再挂一个物块,使得小球A可从图示位置上升并恰好能到达C处,不计摩擦和空气阻力,重力加速度为g.则( )
如图所示,竖直固定的光滑杆上套有一个质量为m的小球A,不可伸长的轻质细绳通过固定在天花板上、大小可忽略的定滑轮O,连接小球A和小球B,虚线OC水平,此时连接小球A的细绳与水平的夹角为60°,小球A恰能保持静止.现在小球B的下端再挂一个物块,使得小球A可从图示位置上升并恰好能到达C处,不计摩擦和空气阻力,重力加速度为g.则( )| A. | 小球B质量为$\frac{\sqrt{3}}{3}$m | |
| B. | 小球B质量为$\frac{2\sqrt{3}}{3}$m | |
| C. | 小球A到达C处时的加速度为g | |
| D. | 小球A上升过程中与小球B速度大小始终相等 |
5. 如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )
如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )
 如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )
如图所示,一正方形物体A内有一圆柱形空腔,此时正以一定的初速度在粗糙的水平面向右减速运动,其质量为M,空腔中有两物体,一个是质量为m的光滑小球B,位于空腔中,其所在位置与圆心的连线与竖直方向的夹角为θ,与A保持相对静止,另一个物体的质量也为m物块C,位于空腔中圆心的正下方,也与A保持相对静止.则下列判断正确的是( )| A. | 物块C对A的作用力大小为mg | |
| B. | 小球B的加速度方向向左,大小为$\frac{g}{tanθ}$ | |
| C. | 地面对A的支持力大小为(M+m)g | |
| D. | 地面与A之间的滑动摩擦因数为tanθ |
10.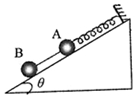 如图所示,A、B两球的质量均为m,轻质弹簧一端固定在斜面顶端,另一端与A球相连,A、B间由一轻质细线连接,倾角为θ的光滑斜面固定在地面上,弹簧、细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )
如图所示,A、B两球的质量均为m,轻质弹簧一端固定在斜面顶端,另一端与A球相连,A、B间由一轻质细线连接,倾角为θ的光滑斜面固定在地面上,弹簧、细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )
 如图所示,A、B两球的质量均为m,轻质弹簧一端固定在斜面顶端,另一端与A球相连,A、B间由一轻质细线连接,倾角为θ的光滑斜面固定在地面上,弹簧、细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )
如图所示,A、B两球的质量均为m,轻质弹簧一端固定在斜面顶端,另一端与A球相连,A、B间由一轻质细线连接,倾角为θ的光滑斜面固定在地面上,弹簧、细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )| A. | B球的加速度沿斜面向下,大小为gsinθ | |
| B. | B球的加速度沿斜面向下,大小为g | |
| C. | A球的加速度沿斜面向上,大小为gsinθ | |
| D. | A球的受力情况未变,加速度为零 |

 如图所示为自行车传动部分的示意图,a为脚蹬,Oa为曲柄,b、d为齿轮,c为链条,e为后轮.已知b轮的齿数为44齿,d轮的齿数为20齿,当b轮转动一周时,d轮带动后轮旋转2.2周,若车轮的直径为26英寸(相当于车轮的周长为2.07m),若骑车人以每分钟60周的转速蹬动b轮,自行车行驶的速度为4.6m/s.
如图所示为自行车传动部分的示意图,a为脚蹬,Oa为曲柄,b、d为齿轮,c为链条,e为后轮.已知b轮的齿数为44齿,d轮的齿数为20齿,当b轮转动一周时,d轮带动后轮旋转2.2周,若车轮的直径为26英寸(相当于车轮的周长为2.07m),若骑车人以每分钟60周的转速蹬动b轮,自行车行驶的速度为4.6m/s. 如图所示,质量为m=2kg的物体放在粗糙的水平面上,物体与水平面间的动摩擦因数为μ=0.2,物体在与水平面成α=37°角大小为10N斜向下的推力F作用下,从静止开始运动,4s末撤去F.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
如图所示,质量为m=2kg的物体放在粗糙的水平面上,物体与水平面间的动摩擦因数为μ=0.2,物体在与水平面成α=37°角大小为10N斜向下的推力F作用下,从静止开始运动,4s末撤去F.(g=10m/s2,sin37°=0.6,cos37°=0.8)求: 水平地面上有质量分别为m和4m的物块A和B,两者与地面间的动摩擦因数均为μ,细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示,初始时,A、B均处于静止状态,并且绳水平拉直,若物块A在水平向右的拉力F作用下向右移动了距离s,重力加速度大小为g,求:
水平地面上有质量分别为m和4m的物块A和B,两者与地面间的动摩擦因数均为μ,细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示,初始时,A、B均处于静止状态,并且绳水平拉直,若物块A在水平向右的拉力F作用下向右移动了距离s,重力加速度大小为g,求: