题目内容
质量均为m的两小球A、B间有压缩的轻、短弹簧,弹簧处于锁定状态,两球的大小尺寸和弹簧尺寸都可忽略,把它们放入固定在水平面上的竖直光滑发射管内,解除弹簧锁定后,B球仍然保持静止,A球能上升的最大高度为R,如图(甲)所示.现在让两球(包括同样锁定的弹簧)沿光滑的半径也为R 的固定半圆槽左端的M 点由静止开始滑下,如图(乙)所示,到达半圆槽的最低点时解除弹簧锁定,求A 球离开半圆槽后能上升的最大高度.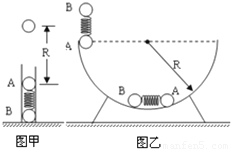
【答案】分析:图甲中,把装置放入固定在水平面上的竖直光滑发射管内,解除弹簧锁定后,弹簧的弹性势能全部转化为A球的动能,A球的动能又转化为重力势能,根据机械能守恒可得到弹簧的弹性势能;
图乙中,系统由水平位置滑到圆轨道最低点时系统的机械能守恒,动量守恒,根据两个守恒列式,求出解除弹簧锁定后,弹簧恢复到原长时A、B的速度,再对A球,由机械能守恒求解最大高度.
解答:解:图甲中,解除锁定后,弹簧将弹性势能全部转化为A球的机械能,则弹簧的弹性势能为:E弹=mgR
较长乙中,AB系统由水平位置滑到圆轨道最低点时速度为v,由机械能守恒定律有:
2mgR= ?2mv2
?2mv2
解除弹簧锁定后,弹簧恢复到原长时,A、B的速度分别为vA、vB,由系统的动量守恒和机械能守恒,则有:
2mv=mvA+mvB
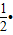 2mv2+E弹=
2mv2+E弹= mvA2+
mvA2+ mvB2
mvB2
解得:vA=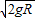 -
-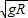 (不符合题意,舍去)
(不符合题意,舍去)
vA=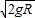 +
+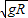
设A球相对于半圆槽口上升最大高度为h,则:
mg(h+R)= mvA2
mvA2
解得:h=( +
+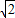 )R≈1.9R
)R≈1.9R
答:A 球离开半圆槽后能上升的最大高度是1.9R.
点评:本题有两种情形,多过程问题,首先要抓住两种情况相等的量:弹簧的弹性势能相等;二要把握乙图中物理规律:系统的机械能守恒和动量守恒进行求解.
图乙中,系统由水平位置滑到圆轨道最低点时系统的机械能守恒,动量守恒,根据两个守恒列式,求出解除弹簧锁定后,弹簧恢复到原长时A、B的速度,再对A球,由机械能守恒求解最大高度.
解答:解:图甲中,解除锁定后,弹簧将弹性势能全部转化为A球的机械能,则弹簧的弹性势能为:E弹=mgR
较长乙中,AB系统由水平位置滑到圆轨道最低点时速度为v,由机械能守恒定律有:
2mgR=
 ?2mv2
?2mv2解除弹簧锁定后,弹簧恢复到原长时,A、B的速度分别为vA、vB,由系统的动量守恒和机械能守恒,则有:
2mv=mvA+mvB
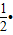 2mv2+E弹=
2mv2+E弹= mvA2+
mvA2+ mvB2
mvB2解得:vA=
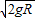 -
-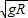 (不符合题意,舍去)
(不符合题意,舍去)vA=
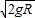 +
+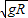
设A球相对于半圆槽口上升最大高度为h,则:
mg(h+R)=
 mvA2
mvA2解得:h=(
 +
+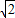 )R≈1.9R
)R≈1.9R答:A 球离开半圆槽后能上升的最大高度是1.9R.
点评:本题有两种情形,多过程问题,首先要抓住两种情况相等的量:弹簧的弹性势能相等;二要把握乙图中物理规律:系统的机械能守恒和动量守恒进行求解.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
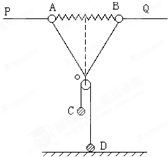 如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.质量为m/2的C球用轻绳跨过质量不计的光滑滑轮与置于水平地面上质量为2m的D球相连,求弹簧的形变量?
如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.质量为m/2的C球用轻绳跨过质量不计的光滑滑轮与置于水平地面上质量为2m的D球相连,求弹簧的形变量? 质量均为m的两小球A、B间有压缩的轻、短弹簧,弹簧处于锁定状态,两球的大小尺寸和弹簧尺寸都可忽略,把它们放入固定在水平面上的竖直光滑发射管内,解除弹簧锁定后,B球仍然保持静止,A球能上升的最大高度为R,如图(甲)所示.现在让两球(包括同样锁定的弹簧)沿光滑的半径也为R 的固定半圆槽左端的M 点由静止开始滑下,如图(乙)所示,到达半圆槽的最低点时解除弹簧锁定,求A 球离开半圆槽后能上升的最大高度.
质量均为m的两小球A、B间有压缩的轻、短弹簧,弹簧处于锁定状态,两球的大小尺寸和弹簧尺寸都可忽略,把它们放入固定在水平面上的竖直光滑发射管内,解除弹簧锁定后,B球仍然保持静止,A球能上升的最大高度为R,如图(甲)所示.现在让两球(包括同样锁定的弹簧)沿光滑的半径也为R 的固定半圆槽左端的M 点由静止开始滑下,如图(乙)所示,到达半圆槽的最低点时解除弹簧锁定,求A 球离开半圆槽后能上升的最大高度.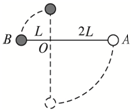 如图所示,质量均为m的两小球A和B用长为3L的轻杆相连,轻杆可绕距A小球2L的轴O在竖直平面内自由转动.现将轻杆拉至水平位置并由静止释放,试求:
如图所示,质量均为m的两小球A和B用长为3L的轻杆相连,轻杆可绕距A小球2L的轴O在竖直平面内自由转动.现将轻杆拉至水平位置并由静止释放,试求: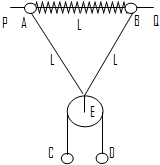 如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.释放C、D后,当C、D球运动时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)
如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.释放C、D后,当C、D球运动时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)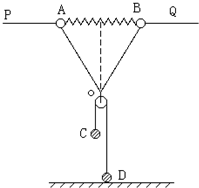 如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.,O的下端为质量不计的光滑定滑轮,质量为m/2的C球用轻绳跨过定滑轮与置于水平地面上质量为2m的D球相连,求弹簧的原长?
如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.,O的下端为质量不计的光滑定滑轮,质量为m/2的C球用轻绳跨过定滑轮与置于水平地面上质量为2m的D球相连,求弹簧的原长?