题目内容
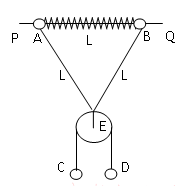
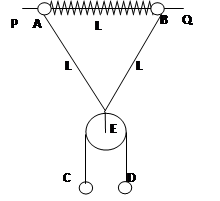
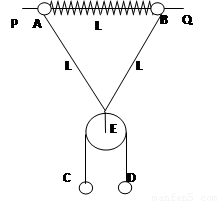
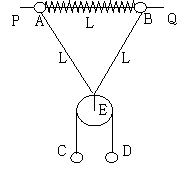
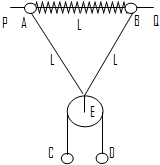 如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.释放C、D后,当C、D球运动时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)
如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.释放C、D后,当C、D球运动时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)求:
(1)C、D球运动时,连接C、D的轻绳中张力T;
(2)求细杆对A球的弹力FA大小;
(3)求弹簧的原始长度?
分析:(1)释放C、D后,C、D都做匀变速运动,加速度大小相等,由整体法根据牛顿第二定律求出它们的加速度大小,再对C球研究,由牛顿第二定律求出连接C、D的轻绳中张力T;
(2)对滑轮研究,竖直方向上力平衡,求出AE线的拉力,再对A球研究,由平衡条件求出细杆对A球的弹力FA大小.
(3)对A球研究,由平衡条件得到弹簧的弹力,由胡克定律求出弹簧的压缩量,再求出弹簧的原始长度.
(2)对滑轮研究,竖直方向上力平衡,求出AE线的拉力,再对A球研究,由平衡条件求出细杆对A球的弹力FA大小.
(3)对A球研究,由平衡条件得到弹簧的弹力,由胡克定律求出弹簧的压缩量,再求出弹簧的原始长度.
解答:解:C、D球在竖直方向做匀变速运动,则它们的加速度大小为:a=
=
g
以C球为研究对象,则有:T-mg=ma
得轻绳的拉力为:T=mg+ma=
mg
(2)对滑轮,设AE线的拉力为T1,有:2T1cos30°=2T
得:T1=
mg
对A球,在竖直方向:FA=mg+T1sin60°
得:FA=
mg
(3)对A球:在水平方向有:F弹=T1cos60°
得:F弹=
mg
弹簧被压缩,所以弹簧原长:L0=L+x=L+
=L+
mg
答:(1)C、D球运动时,连接C、D的轻绳中张力为
mg;
(2)细杆对A球的弹力FA大小为
mg;
(3)弹簧的原始长度是L+
mg.
| 2mg-mg |
| 3m |
| 1 |
| 3 |
以C球为研究对象,则有:T-mg=ma
得轻绳的拉力为:T=mg+ma=
| 4 |
| 3 |
(2)对滑轮,设AE线的拉力为T1,有:2T1cos30°=2T
得:T1=
8
| ||
| 9 |
对A球,在竖直方向:FA=mg+T1sin60°
得:FA=
| 7 |
| 3 |
(3)对A球:在水平方向有:F弹=T1cos60°
得:F弹=
4
| ||
| 9 |
弹簧被压缩,所以弹簧原长:L0=L+x=L+
| F弹 |
| k |
4
| ||
| 9k |
答:(1)C、D球运动时,连接C、D的轻绳中张力为
| 4 |
| 3 |
(2)细杆对A球的弹力FA大小为
| 7 |
| 3 |
(3)弹簧的原始长度是L+
4
| ||
| 9k |
点评:本题中有连接体问题和平衡问题.连接体的加速度大小相等,也可以根据整体法求出加速度,隔离法求解绳子的拉力.

练习册系列答案
相关题目