题目内容
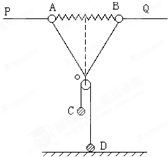 如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.质量为m/2的C球用轻绳跨过质量不计的光滑滑轮与置于水平地面上质量为2m的D球相连,求弹簧的形变量?
如图所示,整个装置处于静止状态,PQ为水平放置的光滑细长杆,质量均为m的两小球 A、B穿于其上.两球用长度均为L的轻线结于O点,A、B球间杆上有一劲度系数为K的被压缩的轻弹簧(在弹性限度内),这时弹簧的长度也为L.质量为m/2的C球用轻绳跨过质量不计的光滑滑轮与置于水平地面上质量为2m的D球相连,求弹簧的形变量?分析:先对滑轮分析,求出绳子OE的拉力,再对结点0受力分析,根据共点力平衡求出AO、BO绳的拉力,然后在对A球受力分析,求出弹簧的弹力,根据胡克定律求出弹簧的形变量,
解答:解: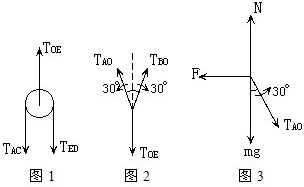 以滑轮为对象,受力如图1.处于平衡状态故有:
以滑轮为对象,受力如图1.处于平衡状态故有:
TOE=2TCE=mg
以O点为对象,受力分析如图2,TAO=TBO,则有
∑F=0
2TAOcos30°=mg
TAO=
以A球为研究对象,受力分析如图3,满足∑F=0
F=TA0Sin30°=
mg
则弹簧的伸长量:x=
=
答:弹簧的形变量为
.
 以滑轮为对象,受力如图1.处于平衡状态故有:
以滑轮为对象,受力如图1.处于平衡状态故有:TOE=2TCE=mg
以O点为对象,受力分析如图2,TAO=TBO,则有
∑F=0
2TAOcos30°=mg
TAO=
| mg | ||
|
以A球为研究对象,受力分析如图3,满足∑F=0
F=TA0Sin30°=
| ||
| 6 |
则弹簧的伸长量:x=
| F |
| K |
| ||
| 6K |
答:弹簧的形变量为
| ||
| 6K |
点评:解决本题的关键选择合适的研究对象,进行受力分析,运用共点力平衡进行求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图所示,整个装置处于静止状态,A、B两球由一根跨过定滑轮的轻绳相连接,A为一带孔小球,穿在光滑固定的竖直杆OD上,且A球与斜面不接触,B与斜面的接触面光滑,C处滑轮摩擦不计,C、B之间的绳与竖直方向成30°角,C、A之间的绳与斜面平行,斜面倾角θ为30°,则A、B两球的质量比为( )
如图所示,整个装置处于静止状态,A、B两球由一根跨过定滑轮的轻绳相连接,A为一带孔小球,穿在光滑固定的竖直杆OD上,且A球与斜面不接触,B与斜面的接触面光滑,C处滑轮摩擦不计,C、B之间的绳与竖直方向成30°角,C、A之间的绳与斜面平行,斜面倾角θ为30°,则A、B两球的质量比为( ) (2011?上饶二模)如图所示,整个装置处于静止状态,A、B两球由一根跨过定滑轮的轻绳相连接,A为一带孔小球,穿在光滑固定的竖直杆OD上,且A球与斜面不接触,B与斜面体的接触面光滑,C处滑轮摩擦不计,C、B之间的绳与竖直方向成30°角,C、A之间的绳与斜面平行,斜面倾角θ为
(2011?上饶二模)如图所示,整个装置处于静止状态,A、B两球由一根跨过定滑轮的轻绳相连接,A为一带孔小球,穿在光滑固定的竖直杆OD上,且A球与斜面不接触,B与斜面体的接触面光滑,C处滑轮摩擦不计,C、B之间的绳与竖直方向成30°角,C、A之间的绳与斜面平行,斜面倾角θ为 ,求此粒子在磁场中运动的时间t。
,求此粒子在磁场中运动的时间t。

 B.1 C.
B.1 C. D.
D.
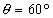 ,求此粒子在磁场中运动的时间t。
,求此粒子在磁场中运动的时间t。