题目内容
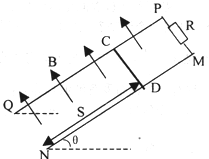如图所示，MN、PQ是两根足够长的平行光滑导轨，两导轨间距为L，导轨平面与水平面的夹角为θ，两导轨间垂直于导轨平面有斜向上的匀强磁场，磁感应强度为B，导轨MP端连有一阻值为R的电阻，其余电阻不计．若将一垂直于导轨，质量为M的金属棒CD在距NQ端为S处由静止释放，则CD棒滑至底端前，会经历加速运动和匀速运动两个阶段．今用大小为F，方向沿斜面向上的恒力把CD棒从NQ由静止开始推至距NQ端为S处，撤去恒力F，棒CD最后又回到NQ端．求CD棒自NQ出发至又回到NQ端的整个过程中，有多少电能通过电阻R转化成内能？
分析：因导轨无摩擦，将CD从NQ推至S高出，然后又回到出发点，在这过程中拉力的功转化为R上的内能和棒的动能；匀速下滑时，重力的功率与电功率相等．
解答：解：因导轨无摩擦，将CD从NQ推至S高出，然后又回到出发点，在这过程中由功能关系：
FS=Q+
m
其中Q是转化为内能的电能，为下滑最后阶段匀速运动的速度．
匀速下滑时，重力的功率与电功率相等，即：mgsinθ?vm=
联立以上两个公式解得：Q=FS-
答：有Q=FS-
电能通过电阻R转化成内能．
FS=Q+
| 1 |
| 2 |
| v | 2 m |
其中Q是转化为内能的电能，为下滑最后阶段匀速运动的速度．
匀速下滑时，重力的功率与电功率相等，即：mgsinθ?vm=
| (BLvm)2 |
| R |
联立以上两个公式解得：Q=FS-
| m3g2R2sin2θ |
| 2B4L4 |
答：有Q=FS-
| m3g2R2sin2θ |
| 2B4L4 |
点评：该题重点考查电磁感应中的能量守恒，所以要注意内能转化的方向和转化关系，属于中档题目．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
（2012?开封模拟）如图所示，MN、PQ为足够长的平行导轨，间距L=O.5m，导轨平面与水平面 间的夹角6=37°，NQ丄MN，NQ间连接有一个R=3Ω的电阻．有一匀强磁场垂直于 导轨平面，磁感应强度为B=1T．将一根质量为m=0.05kg的金属棒放置在导轨上，金属棒的电阻r=2Ω，其余部分电阻不计．现从ab由静止释放金属棒，ab紧靠NQ，金属棒沿导轨向下运动过程中始 终与NQ平行．已知金属棒与导轨间的动摩擦因数μ=0.5，金属棒滑行至cd处时速度大小开始保持不变，cd到ab的距 离为S=2m．（g取=10m/s2）
如图所示，MN、PQ为间距L=0.5m且足够长的平行导轨，NQ⊥MN，导轨 平面与水平面间的夹角θ=37°，NQ间连接一个R=4Ω的电阻．一匀强磁场垂直于导轨平面，磁感应强度B=1T．将一根质量m=0.05kg、电阻r=1Ω的金属棒ab，紧靠NQ放置在导轨上，且与导轨接触良好，导轨的电阻不计．现静止释放金属棒，金属棒沿导轨向下运动过程中始终与NQ平行．已知金属棒与导轨间的动摩擦因数μ=0.5，当金属棒滑行至cd处时已经达到稳定速度，cd离NQ的距离s=0.2m．g取l0m/s2，sin37°=0.6，cos37°=0.8． 问：
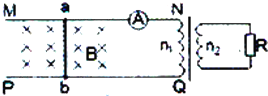如图所示，MN、PQ是两条在水平面内、平行放置的光滑金属导轨，导轨的右端接理想变压器的原线圈，变压器的副线圈与阻值为R=0.5Ω的电阻组成闭合回路，变压器的原副线圈匝数之比n1：n2=2，导轨宽度为L=0.5m．质量为m=1kg的导体棒ab垂直MN、PQ放在导轨上，在水平外力作用下，从t=0时刻开始往复运动，其速度随时间变化的规律是v=2sin| π |
| 2 |
A、在t=1s时刻电流表的示数为
| ||||
| B、导体棒两端的最大电压为1V | ||||
| C、单位时间内电阻R上产生的焦耳热为0.25J | ||||
| D、从t=0至t=3s的时间内水平外力所做的功为0.75J |
如图所示，MN和PQ式固定在水平面内间距L=0.02m的平行金属轨道，轨道的电阻忽略不计，金属杆ab垂直放置在轨道上．两轨道间连接有阻值为R0=1.50Ω的电阻，ab杆的电阻R=0.50Ω，ab杆与轨道接触良好并不计摩擦，整个装置放置在磁感应强度为B=0.50T的匀强磁场中，磁场方向垂直轨道平面向下．对ab杆施加一水平向右的拉力，使之以v=5.0m/s的速度在金属轨道上向右匀速运动．求：