题目内容
6. 如图所示,灯泡A、B都能正常发光,后来由于电路中某个电阻发生断路,致使灯泡A,灯泡B比原来亮一些,则断路的电阻是( )
如图所示,灯泡A、B都能正常发光,后来由于电路中某个电阻发生断路,致使灯泡A,灯泡B比原来亮一些,则断路的电阻是( )| A. | R1 | B. | R2 | C. | R3 | D. | 以上说法都不对 |
分析 首先明确电路中各用电器的连接关系:R2与灯泡B并联,与R1、A串联,再与R3并联.由题意灯泡A变暗了,说明实际功率变小了,灯泡B变亮,说明实际功率增大了.具体故障可将每个选项逐一代入题目检查是否符合题意,从而确定正确选项.
解答 解:A、若R1断路,则电路断开,两灯均不发光;故A错误;
B、若R2断路,则电路中总电阻增大,电流减小,路端电压增大,R1分压增大,电流增大,则流过A的电流减小;灯泡A亮度变暗;故B错误;
C、若R3断路,则总电阻增大,总电流减小,内压减小,路端电压增大,则AB两灯两端的电压均增大;故两灯均变亮;故C正确;
D、因C正确,故D错误;
故选:C.
点评 此题属混联电路的故障问题.解决的关键是在明确电路连接关系的前提下采用“排除法”将每一选项逐一代入题干,检查是否符合题意,最终确定正确选项

练习册系列答案
相关题目
16.关于简谐振动,下列说法正确的是( )
| A. | 如果质点振动的位移与时间的关系遵从正弦函数的规律,这样的振动叫做简谐振动 | |
| B. | 如果质点做简谐振动,则质点振动的动能和弹性势能的总和保持不变 | |
| C. | 回复力F=-kx,是简谐振动的条件,回复力F只能是弹力 | |
| D. | 弹簧振子的振动在考虑空气阻力时,做的也是简谐振动 |
17.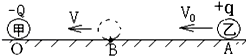 如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
 如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
如图所示,一个电量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电荷量为+q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点时的速度为v,且为运动过程中速度最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )| A. | 点电荷乙从A点运动到B点的过程中,加速度逐渐减小 | |
| B. | OB间的距离为$\sqrt{\frac{kQq}{μmg}}$ | |
| C. | 点电荷乙越过B点向左运动,其电势能仍增多 | |
| D. | 在点电荷甲形成的电场中,AB间电势差UAB=$\frac{μmg{L}_{0}+\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}}{q}$ |
14.在地月系统中,若忽略其他星球的影响,可将月球和地球看成双星系统,即它们在彼此引力作用下绕二者连线上的某点做匀速圆周运动.设想人类能够在月球上生活,为了减轻地球上人口太多的压力,可以不断将人送到月球上居住,假设月球和地球间的距离及他们的总质量均不变,它们的轨道可看成圆,则在该过程中,下列说法正确的是( )
| A. | 地球做圆周运动的轨道半径增大 | B. | 地球做圆周运动的轨道半径减小 | ||
| C. | 月球做圆周运动的角速度不变 | D. | 月球做圆周运动的线速度不断减小 |
11. 如图所示,力F1和F2共同作用在置于水平面上的物体上,F1水平,F2与水平方向夹角为θ,物体在运动过中,力F1与F2的合力做功为W,若物体一直沿水平地面运动,则力F2对物体做功大小为( )
如图所示,力F1和F2共同作用在置于水平面上的物体上,F1水平,F2与水平方向夹角为θ,物体在运动过中,力F1与F2的合力做功为W,若物体一直沿水平地面运动,则力F2对物体做功大小为( )
 如图所示,力F1和F2共同作用在置于水平面上的物体上,F1水平,F2与水平方向夹角为θ,物体在运动过中,力F1与F2的合力做功为W,若物体一直沿水平地面运动,则力F2对物体做功大小为( )
如图所示,力F1和F2共同作用在置于水平面上的物体上,F1水平,F2与水平方向夹角为θ,物体在运动过中,力F1与F2的合力做功为W,若物体一直沿水平地面运动,则力F2对物体做功大小为( )| A. | $\frac{W{F}_{2}}{({F}_{1}+{F}_{2})}$ | B. | $\frac{W{F}_{2}cosθ}{({F}_{1}+{F}_{2})}$ | ||
| C. | $\frac{W{F}_{1}cosθ}{({F}_{1}cosθ+{F}_{2})}$ | D. | $\frac{W{F}_{2}cosθ}{({F}_{1}+{F}_{2}cosθ)}$ |
18. 如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )
如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )
 如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )
如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )| A. | 12 J,2m/s | B. | 0,2m/s | C. | 0,0 | D. | 4J,2m/s |
1. 如图,物块P放在三角形木块Q的光滑斜面上,在外力作用下一起向左作匀速直线运动,现撤去外力,Q仍保持匀速运动,则P相对于地面的运动是( )
如图,物块P放在三角形木块Q的光滑斜面上,在外力作用下一起向左作匀速直线运动,现撤去外力,Q仍保持匀速运动,则P相对于地面的运动是( )
 如图,物块P放在三角形木块Q的光滑斜面上,在外力作用下一起向左作匀速直线运动,现撤去外力,Q仍保持匀速运动,则P相对于地面的运动是( )
如图,物块P放在三角形木块Q的光滑斜面上,在外力作用下一起向左作匀速直线运动,现撤去外力,Q仍保持匀速运动,则P相对于地面的运动是( )| A. | 匀变速直线运动 | B. | 匀变速曲线运动 | ||
| C. | 非匀变速直线运动 | D. | 非匀变速曲线运动 |
2.一个质量为m、电荷量为q的带电粒子,从O点以初速度v0沿平行于电场的方向进入一个场强为E的匀强电场.若不计重力,经过时间t,粒子到达A点时速度恰好为零,则O、A两点间的电势差为( )
| A. | $\frac{{m{v}_{0}}^{2}}{2q}$ | B. | $\frac{{m{v}_{0}}^{2}}{2qE}$ | C. | $\frac{q{E}^{2}{t}^{2}}{2m}$ | D. | $\frac{qE{t}^{2}}{2m}$ |
 在粗糙水平面上竖直放置半径为R=6cm的光滑圆轨道,质量为m=4kg的物块静止放置在粗糙水平面A处,物块与水平面的动摩擦因数μ=0.75,A与B的间距L=0.5m,现对物块施加大小恒定的力F使其沿粗糙水平面做直线运动,到达B处将拉力F撤去,物块沿竖直光滑圆轨道运动,若拉力F与水平面的夹角为θ时,物块恰好沿竖直光滑圆轨道通过最高点,重力加速度g取10m/s2,物块可视为质点,求:
在粗糙水平面上竖直放置半径为R=6cm的光滑圆轨道,质量为m=4kg的物块静止放置在粗糙水平面A处,物块与水平面的动摩擦因数μ=0.75,A与B的间距L=0.5m,现对物块施加大小恒定的力F使其沿粗糙水平面做直线运动,到达B处将拉力F撤去,物块沿竖直光滑圆轨道运动,若拉力F与水平面的夹角为θ时,物块恰好沿竖直光滑圆轨道通过最高点,重力加速度g取10m/s2,物块可视为质点,求: