题目内容
已知地球的自转周期和半径分别为T和R,地球同步卫星A的圆轨道半径为h。卫星B沿半径为r(r<h)的圆轨道在地球赤道的正上方运行,其运行方向与地球自转方向相同。求:
(1)卫星B做圆周运动的周期;
(2)卫星A和B连续地不能直接通讯的最长时间间隔(信号传输时间可忽略)。
(1)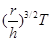 ;(2)
;(2)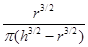 (arcsin
(arcsin +arcsin
+arcsin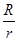 )T
)T
解析试题分析:(1)设卫星B绕地心转动的周期为T′,地球质量为M,卫星A、B的质量分别为m、m′,根据万有引力定律和圆周运动的规律有: =mh
=mh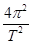 ①
① =m′r
=m′r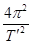 ②
②
联立①②两式解得:T′=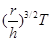 ③
③
(2)设卫星A和B连续地不能直接通讯的最长时间间隔t,在时间间隔t内,卫星A和B绕地心转过的角度分别为α和β,则:α= ×2π,β=
×2π,β=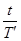 ×2π ④
×2π ④
若不考虑卫星A的公转,两卫星不能直接通讯时,卫星B的位置应在下图中B点和B′点之间,图中内圆表示地球的赤道。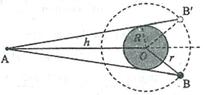
由图中几何关系得:∠BOB′=2(arcsin +arcsin
+arcsin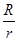 ) ⑤
) ⑤
由③式知,当r<h时,卫星B比卫星A转得快,考虑卫星A的公转后应有:β-α=∠BOB′ ⑥
由③④⑤⑥式联立解得:t=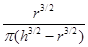 (arcsin
(arcsin +arcsin
+arcsin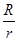 )T
)T
考点:本题主要考查了万有引力定律的应用和空间想象能力问题,属于中档偏高题。

设想在地球赤道平面内有一垂直于地面延伸到太空的轻质电梯,电梯顶端可超过地球的同步卫星高度R(从地心算起)延伸到太空深处,这种所谓的太空电梯可用于低成本地发射绕地人造卫星.假设某物体A乘坐太空电梯到达了图示的B位置并停在此处,与同高度运行的卫星C比较( ) 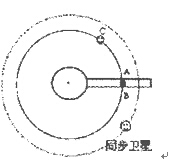
| A.A与C运行的速度相同 |
| B.A的速度大于C的速度 |
| C.A的速度小于C的速度 |
| D.因为不知道质量,故无法比较A与C的速度大小 |
2013年6月13日,北京时间6月13日13时18分,天宫一号目标飞行器与神十飞船在离地面343Km的近圆轨道上进行了我国第5次载入空间交会对接。神舟十号航天员成功开启天宫一号目标飞行器舱门,聂海胜、张晓光、王亚平以漂浮姿态进入天宫一号.下列说法正确的是
| A.航天员以漂浮姿态进入天宫一号,说明航天员不受地球引力作用 |
| B.完成对接后组合体的运行速度小于7.9Km/s |
| C.王亚平在天宫一号中讲课时可以用弹簧秤悬挂测一杯水的重力 |
| D.完成对接后的组合体运行的加速度大于9.8m/s2 |
“嫦娥四号”月球飞船计划在2017年发射升空,现将它与“神舟十号”载人飞船进行类比分析。设月球、地球的质量分别为m1、m2,“嫦娥四号”与“神舟十号”轨道半径分别为 、
、 ,“神舟十号”环绕速度为v,环绕周期为T,则“嫦娥四号”在月球轨道上的环绕速度和环绕周期可表述为
,“神舟十号”环绕速度为v,环绕周期为T,则“嫦娥四号”在月球轨道上的环绕速度和环绕周期可表述为
A. , , | B. , , |
C. , , | D. , , |
长期以来“卡戎星(Charon)”被认为是冥王星唯一的卫星,它的公转轨道半径r1=19600km,公转周期T1=6.39天。2006年3月,天文学家新发现两颗冥王星的小卫星,其中一颗的公转轨道半径r2=48000km,则它的公转周期T2最接近于( )
| A.15天 | B.25天 | C.35天 | D.45天 |
“神舟”七号实现了航天员首次出舱。如图所示飞船先沿椭圆轨道1飞行,然后在远地点P处变轨后沿圆轨道2运行,在轨道2上周期约为90分钟。则下列判断正确的是
| A.飞船沿椭圆轨道1经过P点时的速度与沿圆轨道经过P点时的速度相等 |
| B.飞船在圆轨道2上时航天员出舱前后都处于失重状态 |
| C.飞船在圆轨道2的角速度大于同步卫星运行的角速度 |
| D.飞船从椭圆轨道1的Q点运动到P点过程中万有引力做正功 |
2013年12月11日,“嫦娥三号”携带月球车“玉兔”从距月面高度为100km的环月圆轨道I上的P点变轨,进入近月点为15km的椭圆轨道II,由近月点Q成功落月,如图所示。关于“嫦娥三号”,下列说法正确的是 ( )
| A.沿轨道I运行一周的位移大于沿轨道II运行一周的位移 |
| B.沿轨道II运行时,在P点的加速度小于在Q点的加速度 |
| C.沿轨道II运行的周期大于沿轨道I运行的周期 |
| D.在轨道II上由P点到Q点的过程中机械能增加 |
科学家在望远镜中看到太阳系外某一恒星有一行星,并测得它围绕该恒星运行一周所用的时间为1200 年,它与该恒星的距离为地球到太阳距离的100 倍。 假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周,仅利用以上两个数据可以求出的量有( )
| A.行星质量与太阳质量之比 |
| B.恒星密度与太阳密度之比 |
| C.行星质量与地球质量之比 |
| D.行星运行速度与地球公转速度之比 |