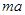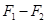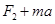题目内容
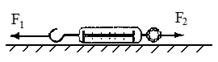
已知一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动。某时刻在传送带适当的位置放上具有一定初速度的物块（如图a所示），以此时为t=0时刻纪录了小物块之后在传送带上运动速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小v1＞v2）。已知传送带的速度保持不变。（g取10 m/s2），则（ ）
| A．0～t1内，物块对传送带做正功 |
| B．物块与传送带间的动摩擦因数为μ，μ＜tanθ |
C．0～t2内，传送带对物块做功为W= |
| D．系统产生的热量大小一定大于物块动能的变化量大小 |
D
解析试题分析: 由图知，物块先向下运动后向上运动，则知传送带的运动方向应向上．0～t1内，物块对传送带的摩擦力方向沿传送带向下，则物块对传送带做负功．故A错误；在t1～t2内，物块向上运动，则有 μmgcosθ＞mgsinθ，得μ＞tanθ．故B错误；0～t2内，由图“面积”等于位移可知，物块的总位移沿斜面向下，高度下降，重力对物块做正功，设为WG，根据动能定理得：W+WG=则传送带对物块做功W≠，故C错误；物块的重力势能减小、动能也减小都转化为系统产生的内能，则由能量守恒得知，系统产生的热量大小一定大于物块动能的变化量大小．故D正确．
考点：动能定理的应用；牛顿第二定律
如图所示，小球在竖直力F作用下将竖直弹簧压缩，若将力F撤去，小球将向上弹起并离开弹簧，直到速度变为零为止，在小球上升的过程中（ ）
| A．小球和弹簧接触阶段加速度先增大再减小 |
| B．小球在离开弹簧时动能最大 |
| C．小球的动能最大时弹性势能为零 |
| D．小球的动能减为零时，重力势能最大 |
有一种杂技表演叫“飞车走壁”。由杂技演员驾驶摩托车沿圆台形表演台的侧壁，做匀速圆周运动。右图中粗线圆表示摩托车的行驶轨迹，轨迹离地面的高度为h。下列说法中正确的是：
| A．h越高，摩托车对侧壁的压力将越大 |
| B．h越高，摩托车做圆周运动的向心力将越大 |
| C．h越高，摩托车做圆周运动的周期将越小 |
| D．h越高，摩托车做圆周运动的线速度将越大 |
如图所示，竖立在水平地面上的轻弹簧，下端与地面固定，将一个金属球放置在弹簧顶端（球与弹簧不粘连），并用力向下压球，使弹簧作弹性压缩，稳定后用细线把弹簧拴牢，烧断细线，球将被弹起，脱离弹簧后能继续向上运动，那么该球从细线被烧断到刚脱离弹簧的这一运动过程中（ ）
| A．球所受合力的值先减小后增大 |
| B．在某一阶段内球的动能减小而它的机械能增加 |
| C．球刚脱离弹簧时的动能最大 |
| D．球刚脱离弹簧时弹簧的弹性势能最小 |
若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球，测出小球的水平射程为
。已知月球半径为
，万有引力常量为
。则下列说法不正确的是
A．月球表面的重力加速度 |
B．月球的质量 |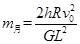
C．月球的第一宇宙速度 |
D．月球的平均密度 |
一质点由静止开始做直线运动，其a-t图象如图所示，下列说法中正确的是( )
| A．1s末质点的运动速度最大 |
| B．4s末质点回到出发点 |
| C．1s末和3s末质点的运动速度相同 |
| D．2s末质点的运动速度为4m/s |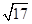
m/s 
m/s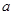 
，那么此弹簧秤的读数是（ ）
