题目内容
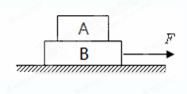
物体在变力F作用下沿水平方向做直线运动,物体质量m=10kg,F随坐标x的变化情况如图所示。若物体在坐标原点处由静止出发,不计一切摩擦。借鉴教科书中学习直线运动时由v-t图象求位移的方法,结合其他所学知识,根据图示的F-x图象,可求出物体运动到x=16 m处时,速度大小为( )
| A.3 m/s | B.4 m/s | C.2 m/s m/s | D.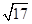 m/s m/s |
C
解析试题分析:在0-4m位移内F恒定,物体做匀加速直线运动,根据牛顿第二定律得;
根据 得:
得: ,对物体在4-16m内运动过程运用动能定理得;
,对物体在4-16m内运动过程运用动能定理得; ,从图中可知
,从图中可知 ,
, ,所以4-16m内力F做功之和为0,所以
,所以4-16m内力F做功之和为0,所以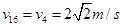 ,C正确;
,C正确;
考点:本题考查了牛顿第二定律、功的计算以及动能定理的应用,要求同学们能根据图象找出有用信息,选取合适的运动过程运用动能定理求解,该题难题适中.

 步步高达标卷系列答案
步步高达标卷系列答案如图所示,MDN为绝缘材料制成的固定的竖直光滑半圆形轨道,半径为R,直径MN水平,整个空间存在方向垂直纸面向外的匀强磁场,磁感应强度为B,一带电荷量为-q,质量为m的小球自M点无初速度下滑,下列说法中正确的是
| A.小球由M点滑到最低点D时所用时间与磁场无关 |
| B.小球滑到D点时,对轨道的压力一定大于mg |
C.小球滑到D点时,速度大小 |
| D.小球滑到轨道右侧时,可以到达轨道最高点N |
已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动。某时刻在传送带适当的位置放上具有一定初速度的物块(如图a所示),以此时为t=0时刻纪录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2)。已知传送带的速度保持不变。(g取10 m/s2),则( )
| A.0~t1内,物块对传送带做正功 |
| B.物块与传送带间的动摩擦因数为μ,μ<tanθ |
C.0~t2内,传送带对物块做功为W= |
| D.系统产生的热量大小一定大于物块动能的变化量大小 |
如图所示,半径r=0.8m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一质量为0. 4kg的小球(小球的半径比r小很多)。现给小球一个水平向右的初速度v0,下列关于在小球的运动过程中说法正确的是(g取10m/s2)( )
| A.v0≤4m/s可以使小球不脱离轨道 |
B.v0≥4 m/s可以使小球不脱离轨道 m/s可以使小球不脱离轨道 |
| C.设小球能在圆轨道中做完整的圆周运动,在最低点与最高点对轨道的压力之差为24N |
| D.设小球能在圆轨道中做完整的圆周运动,在最低点与最高点对轨道的压力之差为20N |
两个质量相同的小球a、b用长度不等的细线拴在天花板上的同一点并在空中同一水平面内做匀速圆周运动,如图所示,则a、b两小球具有相同的
| A.角速度 | B.线速度 | C.向心力 | D.向心加速度 |
如图所示,小球用两根轻质橡皮条悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断某一根橡皮条的瞬间,小球的加速度情况是 
| A.剪断AO瞬间,小球加速度大小是零 |
| B.剪断AO瞬间,小球加速度大小a=gtanα |
| C.剪断BO瞬间,小球加速度大小是零 |
| D.剪断BO瞬间,小球加速度大小a=gcosα |