题目内容
如图所示，小球在竖直力F作用下将竖直弹簧压缩，若将力F撤去，小球将向上弹起并离开弹簧，直到速度变为零为止，在小球上升的过程中（ ）
| A．小球和弹簧接触阶段加速度先增大再减小 |
| B．小球在离开弹簧时动能最大 |
| C．小球的动能最大时弹性势能为零 |
| D．小球的动能减为零时，重力势能最大 |
D
解析试题分析：由题意知，撤去F时，对小球，根据牛顿第二定律可得：
，小球上升的过程中，弹簧形变量x减小，故加速度减小，当弹力
时，加速度减小为零，此时速度最大，动能最大，再向上运动，弹力小于重力
，弹力继续减小，加速度增大，所以小球和弹簧接触阶段加速度先减小后增大，故A错误；由上分析知，动能最大时，小球没有离开弹簧，故B错误；C错误；小球离开弹簧继续减速上升知道速度减小为零，动能为零，此时小球在最高点，重力势能最大，故D正确。
考点：本题考查牛顿第二定律、弹性势能、动能。
“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处，从几十米高处跳下的一种极限运动。某人做蹦极运动，所受绳子拉力F的大小随时间t变化的情况如图所示。将蹦极过程近似为在竖直方向的运动，重力加速度为g。据图可知，此人在蹦极过程中最大加速度约为
| A．g | B．2g | C．3g | D．4g |
某节能运输系统装置的简化示意图如图所示。小车在轨道顶端时，自动将货物装入车中，然后小车载着货物沿不光滑的轨道无初速度下滑，并压缩弹簧。当弹簧被压缩至最短时，立即锁定并自动将货物卸下。卸完货物后随即解锁，小车恰好被弹回到轨道顶端，此后重复上述过程。则下列说法中正确的是( )
| A．小车上滑的加速度小于下滑的加速度 |
| B．小车每次运载货物的质量必须是确定的 |
| C．小车上滑过程中克服摩擦阻力做的功小于小车下滑过程中克服摩擦阻力做的功 |
| D．小车与货物从顶端滑到最低点的过程中，减少的重力势能全部转化为弹簧的弹性势能 |
在水平冰面上，一辆质量为1×103kg的电动雪橇做匀速直线运动，关闭发动机后，雪橇滑行一段距离后停下来，其运动的v—t图象如图所示，那么关于雪橇运动情况以下判断正确的是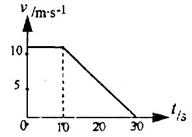
| A．关闭发动机后，雪橇的加速度为-2 m／s2 |
| B．雪橇停止前30s内通过的位移是150 m |
| C．雪橇与水平冰面间的动摩擦因数约为0．03 |
| D．雪橇匀速运动过程中发动机的功率为5×103W |
在以后的运动过程中，圆环运动的速度图象可能是图乙中的（ ）
如图所示，质量形状均相同的木块紧靠在一起，放在光滑的水平面上，现用水平恒力F推1号木块，使10个木块一起向右匀加速运动，则第6号对第7号木块的推力为( ) 
| A．F | B．0.8F | C．0.4F | D．0.2F |
如图所示，MDN为绝缘材料制成的固定的竖直光滑半圆形轨道，半径为R，直径MN水平，整个空间存在方向垂直纸面向外的匀强磁场，磁感应强度为B，一带电荷量为－q，质量为m的小球自M点无初速度下滑，下列说法中正确的是
| A．小球由M点滑到最低点D时所用时间与磁场无关 |
| B．小球滑到D点时，对轨道的压力一定大于mg |
C．小球滑到D点时，速度大小 |
| D．小球滑到轨道右侧时，可以到达轨道最高点N |
已知一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动。某时刻在传送带适当的位置放上具有一定初速度的物块（如图a所示），以此时为t=0时刻纪录了小物块之后在传送带上运动速度随时间的变化关系，如图b所示（图中取沿斜面向上的运动方向为正方向，其中两坐标大小v1＞v2）。已知传送带的速度保持不变。（g取10 m/s2），则（ ）
| A．0～t1内，物块对传送带做正功 |
| B．物块与传送带间的动摩擦因数为μ，μ＜tanθ |
C．0～t2内，传送带对物块做功为W= |
| D．系统产生的热量大小一定大于物块动能的变化量大小 |