题目内容
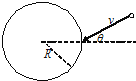
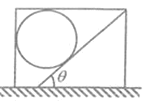
【题目】如图，水平地面上的矩形箱子内有一倾角为θ的固定斜面，斜面上放一质量为m的光滑球。静止时，箱子顶部与球接触但无压力。箱子由静止开始向右做匀加速运动，然后改做加速度大小为a的匀减速运动直至静止，经过的总路程为s，运动过程中的最大速度为v。下列说法正确的是（ ）
A.小球加速运动时的加速度
B.小球加速运动时的加速度
C.若
，减速阶段箱子左壁给小球的支持力大于0
D.若，减速阶段箱子顶部给小球的作用力
【答案】BD
【解析】
由题意可知考查运动学公式应用，牛顿第二定律的综合应用，据此分析计算可得。
AB．设加速度为a′，由匀变速直线运动的公式：
加速阶段：s1=
减速阶段：s2=
得：
s=s1+s2=
解得加速阶段的加速度为：
a′=
；
故A错误，B正确；
CD．设小球不受车厢的作用力，应满足：水平方向：
Nsinθ=ma
竖直方向：
Ncosθ=mg
解得：a=gtanθ
减速时加速度的方向向左，此加速度有斜面的支持力N与左壁支持力共同提供，当a＞gtanθ时，
左壁的支持力等于0，此时小球的受力如图，
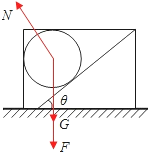
水平方向由牛顿第二定律可得
Nsinθ=ma
竖直方向合力为零
Ncosθ-F=mg
解得：
F=macotθ-mg，
故C错误，D正确；
【题目】现有一质量均匀分布的直杆，绕通过垂直于直杆的水平转轴转动时形成一个摆，称为复摆，如图所示．复摆的周期可以表示为T＝2π
，其中m为直杆的质量，g为重力加速度，h为转轴到直杆质量中心的距离，I为直杆对转轴的转动惯量（描述物体绕转轴转动时的惯性）．当h＝0时，I＝ml2，其中l称为直杆绕通过质量中心且垂直于直杆的水平转轴转动时的回转半径．一般情况下，复摆对转轴的转动惯量可以表示为I＝ml2+mh2，右表为实验中测量的一组h和复摆周期T的值，请用作图法求回转半径l和实验室当地的重力加速度g（要求保留小数点后两位有效数字）
T（s） | 1.56 | 1.51 | 1.50 | 1.53 | 1.54 | 1.59 |
h（m） | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 |
