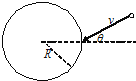
[题目]地面上有一半径为R.深度为h的圆筒形竖井．如图所示.一小球在地面上以水平速度v沿着与井口半径成θ角的方向运动并落入井中．小球与井壁及井底的碰撞均为弹性碰撞.且无摩擦．设小球与井壁碰撞次数为m.与井底碰撞次数为n后.恰能够回到地面上运动.求小球的运动速度v的表达式．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】地面上有一半径为R、深度为h的圆筒形竖井．如图所示，一小球在地面上以水平速度v沿着与井口半径成θ角的方向运动并落入井中．小球与井壁及井底的碰撞均为弹性碰撞，且无摩擦．设小球与井壁碰撞次数为m，与井底碰撞次数为n后，恰能够回到地面上运动，求小球的运动速度v的表达式．

【答案】

【解析】

由题意可知，水平速度运动的时间，与小球垂直方向运动的时间是相等的．小球与井壁及井底的碰撞均为弹性碰撞，且无摩擦，所以小球水平速度不会变，竖直方向的加速度为g，且下降时初速为0，上升时末速为0．

由：小球与井壁碰撞次数为m，则：小球水平运动的总路程为：2（m+1）Rcosθ （也就是弦长的m+1倍），

所用时间：t＝…（1）

由：小球与井底碰撞次数为n，则：小球竖直方向每次上升和下降的时间之和都为：2（碰撞小球下降和上升各一次），

所用总时间：t＝2n…（2）

综合（1）、（2）式，可得：v＝ Rcosθ．

练习册系列答案

（1）求夯头A离地时刻重球C的速率。

（2）忽略打夯机其他部分的牵连和影响，仅以图b所示的模型计算，从离地时刻算起，经过多长时间，A、C组成的系统的质心上升到最高点？

【题目】如图所示，一金属环套在固定的光滑杆上．金属环通过跨过定滑轮的轻绳在外力F作用下，沿杆缓慢上滑，该过程中金属环对杆的作用力为N．则（　　）

A. F一直增大，N先减小后增大

B. F一直在增大，N一直增大

C. F先减小后增大，N一直增大

D. F先减小后增大，N先减小后增大

【题目】如图，水平地面上的矩形箱子内有一倾角为θ的固定斜面，斜面上放一质量为m的光滑球。静止时，箱子顶部与球接触但无压力。箱子由静止开始向右做匀加速运动，然后改做加速度大小为a的匀减速运动直至静止，经过的总路程为s，运动过程中的最大速度为v。下列说法正确的是（　　）

A.小球加速运动时的加速度

B.小球加速运动时的加速度

C.若，减速阶段箱子左壁给小球的支持力大于0

D.若，减速阶段箱子顶部给小球的作用力

【题目】如图所示为静宁一中两位同学探究“物体的加速度与其质量、所受合外力的关系” 的实验装置图．

（1）实验中，两位同学安装好实验装置后，首先平衡摩擦力，他们将长木板的一端适当垫高些后，在不挂砝码盘的情况下，使小车靠近打点计时器后，先接通电源，后用手轻拨小车，小车便拖动纸带在木板上自由运动。若打点计时器第一次在纸带上打出的计时点越来越稀疏（从打出的点的先后顺序看），则第二次打点前应将长木板底下的小木块垫的比原先更加_______（选填“高”或“低”）些；重复以上操作步骤，直到打点计时器在纸带上打出一系列___________的计时点，便说明平衡摩擦力合适。

（2）平衡摩擦力后，在____________的条件下，两位同学可以认为砝码盘(连同砝码)的总重力近似等于小车的所受的合外力。(已知小车的质量为M，砝码盘（连同砝码）的总质量为m)

（3）接下来，这两位同学先保持小车的质量不变的条件下，研究小车的加速度与受到的合外力的关系；右图为某次操作中打出的一条纸带，他们在纸带上标出了5个计数点，在相邻的两个计数点之间还有4个点未标出，图中数据的单位是cm。实验中使用的是频率f＝50 Hz的交变电流．根据以上数据，可以算出小车的加速度a＝________m/s2。(结果保留三位有效数字)

（4）然后，两位同学在保持小车受到的拉力不变的条件下，研究小车的加速度a与其质量M的关系。他们通过给小车中增加砝码来改变小车的质量M，得到小车的加速度a与质量M的数据，画出图线后，发现：当较大时，图线发生弯曲。于是，两位同学又对实验方案进行了进一步地修正，避免了图线的末端发生弯曲的现象，那么，两位同学的修正方案可能是（____）

A．改画a与(M＋m)的关系图线 B．改画a与的关系图线

C．改画a与的关系图线 D．改画a与的关系图线

（5）探究“物体的加速度与其质量、所受合外力的关系”实验完成后，两位同学又打算测出小车与长木板间的动摩擦因数。于是两位同学先取掉了长木板右端垫的小木块，使得长木板平放在了实验桌上，并把长木板固定在实验桌上，具体的实验装置如图所示；在砝码盘中放入适当的砝码后，将小车靠近打点计时器，接通电源后释放小车，打点计时器便在纸带上打出了一系列的点，并在保证小车的质量M、砝码（连同砝码盘）的质量m不变的情况下，多次进行实验打出了多条纸带，分别利用打出的多条纸带计算出了小车运动的加速度，并求出平均加速度，则小车与长木板间的动摩擦因数=________。（用m、M、、g表示）