题目内容
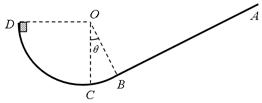
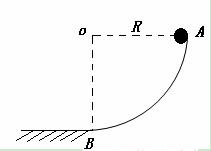
(15分)如图所示,粗糙斜面AB与竖直平面内的光滑圆弧轨道BCD相切于B点,圆弧轨道的半径为R,C点在圆心O的正下方,D点与圆心O在同一水平线上,∠COB=θ。现有质量为m的物块从D点无初速释放,物块与斜面间的动摩擦因数为μ,重力加速度为g。求:
(1)物块第一次通过C点时对轨道压力的大小;
(2)物块在斜面上运动离B点的最远距离。
(1)物块第一次通过C点时对轨道压力的大小;
(2)物块在斜面上运动离B点的最远距离。

(1)3mg
(2)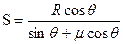
(2)
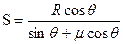
(1)物块从D到C,根据机械能守恒定律,得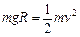 (3分),
(3分),
物块经C点,根据牛顿第二定律,得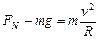 (3分)
(3分)
由以上两式得支持力大小FN="3mg" (2分)
由牛顿第三定律得,物块对轨道的压力大小为3mg (1分)
(2)小物体通过圆弧轨道后,在斜面上运动到最大距离S时速度为0,由动能定理可得
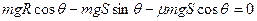 (4分)
(4分)
故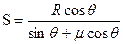 (2分)
(2分)
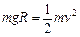 (3分),
(3分),物块经C点,根据牛顿第二定律,得
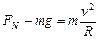 (3分)
(3分)由以上两式得支持力大小FN="3mg" (2分)
由牛顿第三定律得,物块对轨道的压力大小为3mg (1分)
(2)小物体通过圆弧轨道后,在斜面上运动到最大距离S时速度为0,由动能定理可得
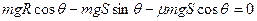 (4分)
(4分)故
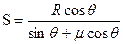 (2分)
(2分)
练习册系列答案
相关题目
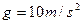 )求:
)求:
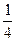 圆管轨道,B、E间是粗糙的水平平台,管道B、E、C端的下表面在同一水平线上且切线均为水平方向。现让质量m=0.5Kg的闪光小球(可视为质点)从A点正上方的Q处自由落下,从A点进入轨道,依次经过
圆管轨道,B、E间是粗糙的水平平台,管道B、E、C端的下表面在同一水平线上且切线均为水平方向。现让质量m=0.5Kg的闪光小球(可视为质点)从A点正上方的Q处自由落下,从A点进入轨道,依次经过 =0.4m,“O”字形圆形轨道半径
=0.4m,“O”字形圆形轨道半径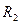 =0.02m。Q点距A点高H=5m,到达“O”字形轨道最低点P时的速度为10m/s,,取g=10m/s2。求:
=0.02m。Q点距A点高H=5m,到达“O”字形轨道最低点P时的速度为10m/s,,取g=10m/s2。求:


 的滑块在倾角为
的滑块在倾角为 的斜面上,从
的斜面上,从 点由静止下滑,到
点由静止下滑,到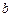 点接触到一个轻弹簧,滑块压缩弹簧到
点接触到一个轻弹簧,滑块压缩弹簧到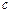 点开始弹回,返回
点开始弹回,返回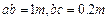 ,那么在整个过程中( )
,那么在整个过程中( )
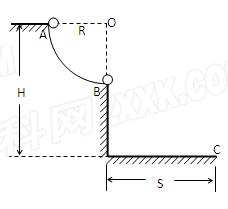
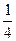 圆弧光滑轨道的A点,圆弧半径为
圆弧光滑轨道的A点,圆弧半径为 R,OB沿竖直方向,
R,OB沿竖直方向, 上端A距地面高为H,现让小球从A点由静止释放,最后落在地面上C点
上端A距地面高为H,现让小球从A点由静止释放,最后落在地面上C点 处,不计空气阻力,求:
处,不计空气阻力,求: