Question

【题目】如图所示，一轻弹簧一端同定在倾角为37°的固定光滑直轨道AD的底端AB处，另一端若自由伸长则位于C点，另一端若固定连接一质量为m的小木块，小木块处于B点时恰静止．直轨道与﹣半径为r=0.5R的光滑圆弧轨道相切于D点，E点为圆弧轨道的最高点（且过E点的切线水平）．BC=CD=R，A、B、C、D、E均在同一竖直面内．质量为m的一小铁块自D点由静止开始下滑，到达B点后与小木块碰撞，碰撞时间极短，碰撞后共同压缩弹簧，此后运动过程中小铁块与小木块恰不分离．轻弹簧始终处于弹性限度内，重力加速度大小为g，（取sin37°=0.6．cos37°=0.8）求：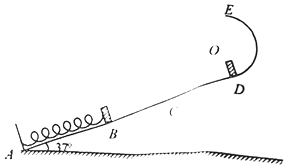

（1）小铁块即将与小木块碰撞时的速率为多大；
（2）小铁块即将与小木块碰撞时弹簧的弹性势能为多大；
（3）若小铁块具有沿直线轨道向下的初速度，小铁块的初速度至少为多大．与小铁块碰撞后，才能沿着圆弧轨道运动到E点．

Answer 1

【答案】
（1）解：小铁块沿直轨道下滑时，根据机械能守恒定律有

mg2Rsin37°=

可得 v1=

答：小铁块即将与小木块碰撞时的速率为 ；

（2）小铁块与小木块碰撞前后，由于碰撞时间极短，动量守恒，取沿斜面向下为正方向，由动量守恒定律有

mv1=2mv2．

碰后，小铁块与小木块共同压缩弹簧，直至速度减小至零后被反间向上运动，当轻弹簧恰恢复原长时，小铁块与小木块即将分离，故此时小铁块和小木块的速度均为零，根据机械能守恒定律有

+Ep=2mgRsin37°

解得小铁块即将与小木块碰撞时弹簧的弹性势能为 Ep=0.6mgR

答：小铁块即将与小木块碰撞时弹簧的弹性势能为0.6mgR；

（3）设小铁块的初速度为v0．小铁块沿直轨道下滑时，根据机械能守恒定律有

+mg2Rsin37°=

小铁块与小木块碰撞过程，由动量守恒定律有

mv1′=2mv2′

碰后，小铁块与小木块共同压缩弹簧，直至速度减小至零后被反间向上运动，当轻弹簧恰恢复原长时，小铁块与小木块即将分离，故此时小铁块和小木块的速度均为零，根据机械能守恒定律有

+Ep=2mgRsin37°+

小铁块与小木块分离后沿CDE恰好运动到E点的过程，由机械能守恒定律有

=mg（Rsin37°+rcos37°+r）+

在最高点E，由重力等于向心力有

mg=m

联立解得 v0=

答：小铁块的初速度至少为 ，与小铁块碰撞后，才能沿着圆弧轨道运动到E点．

【解析】（1）以小铁块为研究对象利用铁块下滑时，机械能守恒求出到达底端时的速度。
（2）铁块和木块碰撞的过程中满足动量守恒先根据动量守恒，求出两物块儿相碰后供述的速度，再根据机械能守恒求铁块被弹出时弹性势能的转换量。（3）小铁棍儿言之轨道下滑利用动能定理，列方程求小铁块的初速度，碰撞过程中动量守恒弹簧弹开五块的过程中，机械能守恒分离后小木块儿，运动过程中机械能守恒，再结合最高点和外力等于向心力列方程组求解即可。